In this problem, we will use the word "Gnomon" to describe a rectangle which has another rectangle cut out of one of its corners, like this:



I can make gnomons by joining small squares on a grid, so that the areas of my gnomons are all Fibonacci numbers. Fibonacci numbers belong to a sequence where each new number is made by adding together the last two numbers in the sequence - $1,1,2,3,5,8,13...$.

Check that you understand how the sequence works before going any further.

Here is a picture showing the first few gnomons with areas $3,5,8,13$ and $21$



These gnomons are special because each one is made by fitting together the previous two gnomons.For example:



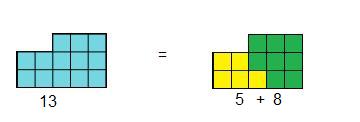
Investigate ways of making each gnomon in the Fibonacci sequence by reflecting and rotating the previous two gnomons to fit them together. 

Can you describe how the tenth and eleventh gnomons in my sequence would fit together to make gnomon twelve?

I have noticed that the edges of my gnomons always seem to be Fibonacci numbers. For example, the fifth gnomon in the picture above has two sides with length $2$, two sides with length $3$ and two sides with length $5$.
$2,3$ and $5$ are all Fibonacci numbers. Will this always be the case?

How could you use Fibonacci numbers to work out perimeters of larger gnomons?