Copyright © University of Cambridge. All rights reserved.
'Weights' printed from https://nrich.maths.org/
Show menu
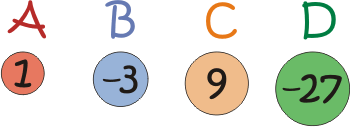
Imagine you have two of each of the 'weights' above.
Different combinations of the weights available allow you to make different totals.
For example:
$B + 2C = 15$
$A + 2B + C = 4$
$2A + B + 2C + D = -10$
The largest total you can make is $20$ (check you agree).
The smallest total you can make is $-60$ (again, check you agree).
Can you make all the numbers in between?
Is there always a unique way of producing a total, or can different combinations produce the same total?
Extension:
If you are allowed just three different weights this time ($E$, $F$ and $G$), and at least one must be a negative weight, and you are now allowed to have up to three of each, you could choose:
$F = -4$
$G = 5$
You could make $7$ and $-10$:
$2E + 3F =$ $-10$
Choose your three weights and test out which totals you can make.
Which set of three weights ($E$, $F$ and $G$) allows you to make the largest range of totals with no gaps in between?
With thanks to Don Steward, whose ideas formed the basis of this problem.