Two equilateral triangles can be put together in one way only, if they must touch all along a side:

These isosceles triangles of the same area can be put together in more than one way.

Remember that reflection can be used as well as rotation when finding the ways.

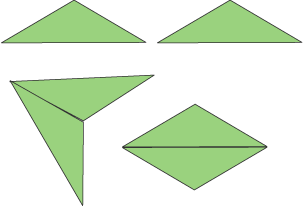
Can you find any other ways?

You could cut out triangles from these sheets.

These triangles are half of the above equilateral and isosceles triangles:

In how many ways do you think two of these can be put together using, reflection as well as rotation, if same-sized sides must touch the full length of the side?

Can you give any reasons for this?

You could cut some of your other triangles in half to test out your prediction.

Can you find a triangle such that two identical copies of it can be put together in more ways keeping to the rule that same-sized sides must touch the full length of the side?