Back in August $1998$ we had a challenge called Pebbles and this investigation could have grown out of it.

We are looking at making squares from several points. So you might like to think of these dots or points:-

Whichever way you care to think about them, we are going to make some squares.
The squares are made by first drawing just one side, always starting that one side from the bottom left-hand square as shown below:

So we might start with this one:-

 

... and draw the rest of the square in by making sure that the sides are at right angles and of the same length - things that you know about squares!

That would give us:

This would be the smallest square that we can make from drawing a line from the bottom left-hand corner to one of the other dots.

We can of course draw other starting lines, such as:

and another such as:
These would lead to squares that would be:

I wonder what size these squares are compared with the first smallest square?

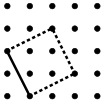
Your challenge is to make more and more squares by using your starting side (roughly in the lower left-hand part) to other points marked in the $5$ by $5$ arrangement.

The investigation is about ways of finding out the areas of all these squares. You do not need any special knowledge but you may need lots of squared paper and a pair of scissors. You may be wanting to use a piece of cut-out card. I guess you'll need a chance to discuss this with friends.

When you've got all your areas sorted out you could continue this investigation by looking at the answers you've got and seeing if there are any special things about them ... I expect there are ... there usually are in these sorts of challenges.