Numbers Numbers Everywhere!

'Numbers Numbers Everywhere!' printed from https://nrich.maths.org/

Show menu

I think it's a good idea to take some number work from the numbers we see in the world around us. We often do lots of things related to the practical when we have to do some counting or tallying to see how many articles there are, but I'm thinking more of seeing actual Numerals about the place. We see digital displays of the time and prices [petrol prices displayed on the road side], we see numbers on clocks, houses and pages.

(A) But I'd like to start with the numbers we see on calendars.

Calendar Activities, from Jan $2001$ may be a good article and series of activities to start with.

This article suggests you don't get rid of your old calendars. The activities, using cut up dates from the calendar, provide numbers to practise skills that need re-visiting. The children choose a page from an old calendar and they chose from that page some numbers from which they are set various challenges.

--------------------

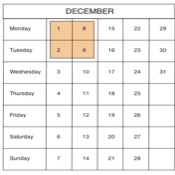
Calendar Patterns, from Jan $2000$

This activity is a great example of how patterns and numbers may be investigated in the context of a page from a calendar and doing some observation and calculations related to how the numbers appear.

--------------------

Calendar Calculations, from Jan $2001$

As well as being used as a follow on from Calendar Patterns it could be revisited several times, trying different approaches each time. The children can discuss discoveries and suggest new things to try. It uses the dates within a week and sets some challenges for pupils to solve.

--------------------

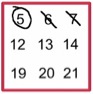
Calendar Capers, from Jan $2002$.

In investigating a square of nine numbers found on a calendar the pupils are asked to identify various relationships using some "game type" moves. They are asked to find any similarity between the three by three square and the totals they get in the rows and columns and the four by four square. Based on the results, they can be asked about the predictions can be made about the sum of the right and left columns or the top and bottom rows. Then there are general questions like; Will it matter what month is chosen? What if a different square of numbers is chosen? What is the largest square that can be found in a month? What would happen if they changed from investigating a square to investigating a rectangle? What if, for example, a $3x4$ rather than a $4x3$ rectangle is used?

--------------------

(B) What about the clocks that we see around us? There's both the digital and analogue to explore. Have a look at;

Times, from Aug $1999$

This activity explores the way that numbers are displayed on a digital clock. It involves a lot of spatial awareness and suggests that pupils look for further interesting numeral arrangements. This can be done by "trial and error" but promotes systematic approaches and can involve some astute thinking.

--------------------

Clock Face, from Nov $1998$

This problem requires logical and creative thinking. It is also an intriguing and challenging way to practise addition and subtraction. The children are asked to look at an analogue clock face and asked to consider the numbers $1$ to $12$.

--------------------

Clock Squares, from March $2000$

This explores the whole area of arithmetic that counts in an alternative way - modulo or clock arithmetic. It enables a lot of number work to be done with what appears to be single digit numbers.

--------------------

Clocked, from Nov $2000$

This challenges with the question - Is it possible to rearrange the numbers 1, 2 ...12 around a clock face in such a way that every two numbers in adjacent positions differ by any of 3, 4 or 5 hours?

--------------------

Clocks, from July $2000$.

This challenges by showing mirror images and asking what the time is. There's opportunity to take this much further.

--------------------

(C)

Calcunos, from July $1999$

This puts together an investigation around anything that displays digital numbers, such as time, money, car instrument displays, counting devices, etc. It involves counting "light-bars".

--------------------

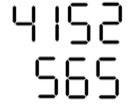
(D)

Then there are the pages in books for older children.

Page Numbers, Jan $1999$

A good number investigation that is centred around the numbering of pages in a book which is very easy to take further.

--------------------

and a general one on consecutive numbers as found in pages of a book called Consecutive Numbers (Nov $1997$).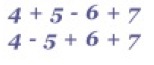

--------------------

(E) Finally, House Numbers.

Street Sequences (March $2007$, April $2007$)

This explores addition of different combinations of nearby house numbers.

--------------------

So, there are probably other places around where you are where there are numbers that can be explored. Have a go at these activities and look around for other examples of numerals to be found in our homes and outside. Many of these activities have generated some interesting patterns of numbers that may be explored further by using Digital Roots - this article on them may help.

This article, slightly edited, also appears in Primary Mathematics, a journal published by The Mathematical Association.

Here is a PDF version of this article.