Semicircle in a Semicircle

'Semicircle in a Semicircle' printed from https://nrich.maths.org/

Show menu

Let T be the centre of the semicircle with diameter QR and let OT produced meet the circumference of the larger semicircle at U .
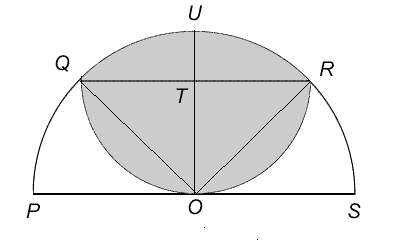
Semicircular arcs solution
By symmetry, we note that OT is perpendicular to QR . As TR = TO = TQ (radii of the same semicircle), triangles ORT and OQT are both isosceles, right-angled triangles. So QOR is a right angle.

By Pythagoras' Theorem: QR ² = OQ ² + OR ² = 2 ² + 2 ² = 8. So $QR = \sqrt8$ = $2\sqrt2$ and the radius of semicircle QOR is $\sqrt2$.

The area of the shaded region is equal to the area of semicircle QOR plus the area of the quadrant bounded by OQ , OR and arc QUR less the triangle OQR .

So the required area is $\frac12 \pi (\sqrt2)^2$ + $\frac14 \pi 2^2$ - ($\frac12 \times 2 \times 2$) = $\pi + \pi - 2$ = $2\pi$ - 2.

This problem is taken from the UKMT Mathematical Challenges.

You can find more short problems, arranged by curriculum topic, in our short problems collection.