 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Four Go



Draw a number line on a piece of paper, marked from $0$ to $20$, like this:

(You could print off this sheet of number lines.)
This challenge is a game for two players. The first player chooses two numbers in this grid and either multiplies or divides them.
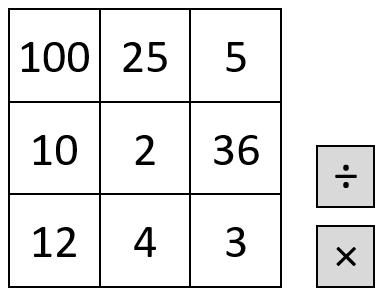
They then mark the answer to the calculation on the number line. The second player then chooses two numbers and either $\times$ or $\div$, and marks that number in a different colour on the number line.
If the answer is too big or too small to be marked on the number line, the player misses a go.
The winner is the player to get four marks in a row with none of their opponent's marks in between.
What good ways do you have of winning the game?
Does it matter if you go first or second?
[This game is adapted from a SMILE Centre card.]