Watch the film below.

Try to describe what happens in the film to someone else.

Imagine the dot starts at the point (1,0), turns through $20^\circ$ and then stops:


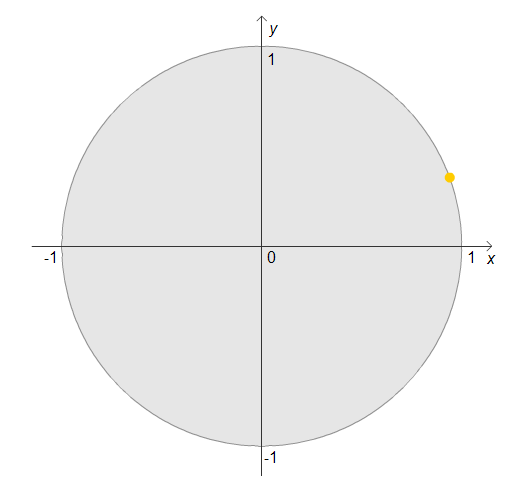
If the point now carries on, through how many degrees must it turn to finish the same height above or below the horizontal axis as it was when it had gone through $20^\circ$?

Can you find a general rule for explaining when the dot will be this same distance from the horizontal axis?

You might like to try Round and Round and Round after this problem.