What do you notice about these two front doors?

Where I live, the houses in many streets are numbered like this, so that the odd numbers are on one side of the road, and the even numbers on the other.

Here is a picture of one side of an imaginary street, with the houses numbered in that way:

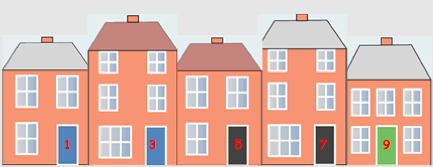
Viewed from above, the house numbers along the street could look like this:

Imagine walking down this street and adding the house numbers in various ways...

You could start with adding in pairs across the street like this:

Have a go.
What do you notice about the answers to your addition calculations?
Can you explain why these patterns occur?

You could change the grouping of houses in different ways. How about:
 

What happens now?
Can you explain any patterns you notice?

Perhaps the houses are already grouped in some way, for example they may all be semi-detached:

You could add houses that are joined, so on one side of the street the totals are 4, 12, 20... and the other side are 6, 14, 22...

You could continue this and explore it further.

You will have your own ideas about what to explore. For inspiration, why not take a walk down a street near you?

Let us know what you investigate, whether it is one of the suggestions above, or something you have come up with yourself.
We would love to hear about the patterns you see, and your explanations for why those patterns occur.