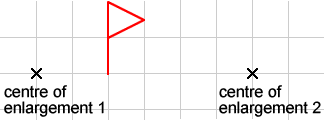
You might find it helpful to copy the diagram onto dotty paper.

Enlarge the flag by a scale factor of $2$ about the first centre of enlargement. Now enlarge the resulting flag by a scale factor of $\frac{1}{2}$ about the second centre of enlargement. Can you find a single transformation that takes the first flag to the last flag?

Try this with the flag in different positions, and with different centres of enlargement. Describe what will happen for any two centres of enlargement and a flag in any position.

Now try changing the scale factors so that the first enlargement is by scale factor $3$ and the second by scale factor $\frac{1}{3}$. Try some other similar pairs (remembering that if the first scale factor is $k$ then the second one should be $\frac{1}{k}$).

Describe what will happen if the first scale factor is $k$ and the second $\frac{1}{k}$?