Take 36 cubes.

Challenge 1

How many different blocks can you make? For example 6 by 6 by 1, or 3 by 6 by 2.

Just how many different ones can you find?

Challenge 2

Try growing different pyramids of cubes which in turn generate different sequences of numbers. Look at the pictures below this table and see if you can work out how the table has been filled in.

 

	1	2	3
A	1	3	5
B	1	4	10
C	1	5	14

 

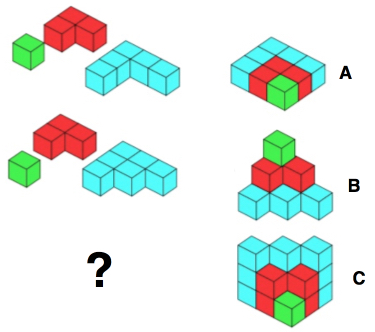
• Can you continue the table?
• What patterns do you notice?
• Can you explain why these patterns occur?