You might like to try Transformations on a Pegboard before looking at this problem. Here are some ideas to take this activity some stages further.

You may like to use this interactive pegboard to try out your ideas. Read underneath the interactivity for the challenges!

Choose the size of your pegboard then select the line tool and click on two dots to draw a line between them. 




One of the challenges was, 'By moving just one peg can you make a right-angled triangle?'. Well, I had a go starting the same way:



Here are two I found moving one peg each time (from the original):







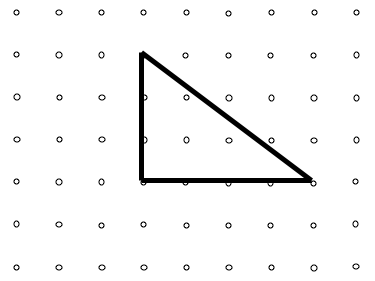
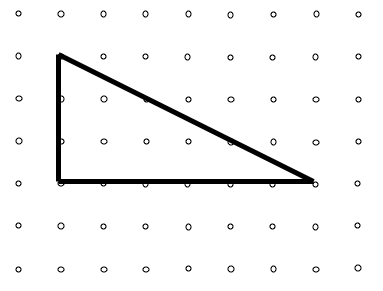
And so on and so on ...
How many different right-angles triangles can you get if you stick to a grid of $7$ rows of dots and $9$ columns of dots?

The triangle started off having a base of $6$ and was $3$ high.
Look at the other triangles you have found that have this same base and height.
What can you say about the areas of this set of triangles?
(You might like to draw some more triangles with a base of $6$ and a height of $3$ which don't have right angles to see what that adds to your thoughts and ideas.)