Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Semi-regular Tessellations
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Goeun from Bangok Patana School in Thailand sent in this solution, which includes 8 semi-regular tesselations. Can Goeun be sure to have found them all?
Firstly, there are only three regular tessellations which are triangles, squares, and hexagons. To make a regular tessellation, the internal angle of the polygon has to be a diviser of 360. This is because the angles have to be added up to 360 so it does not leave any gaps. For example, we can make a regular tessellation with triangles because 60 x 6 = 360.
Students from Cowbridge Comprehensive School in Wales used this spreadsheet to convince themselves that only 3 polygons can make regular tesselations.
Goeun continued:
We can prove that a triangle will fit in the pattern {3, 4, 3, 3, 4} [given in the problem] because 360 - (90 + 60 + 90 + 60) = 60 which is the internal angle for an equilateral triangle.
There are 8 semi-regular tessellations in total. We know each is correct because again, the internal angle of these shapes add up to 360.
For example, for triangles and squares, 60 $\times$ 3 + 90 $\times$ 2 = 360.
- Triangles & Squares
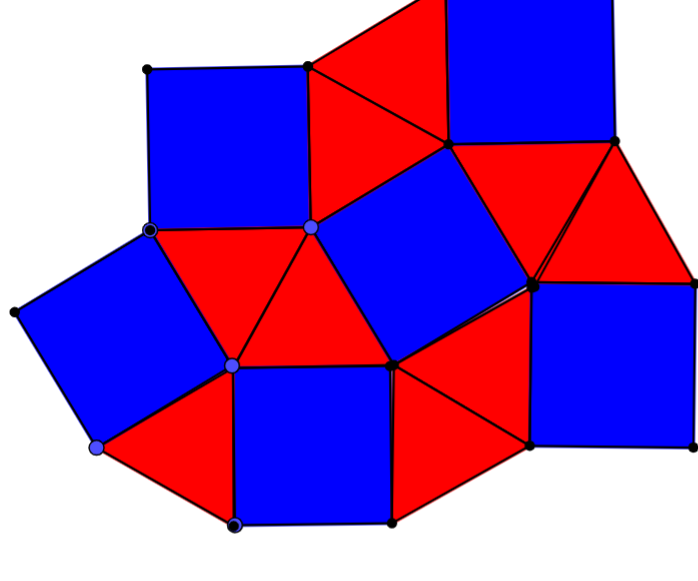
- Triangles & Squares (but a different pattern)
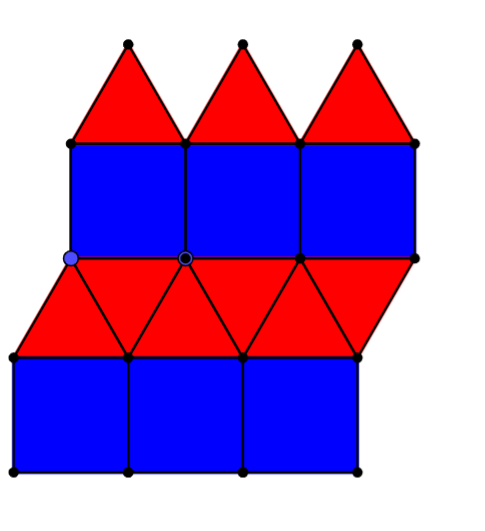
- Hexagons & Triangles
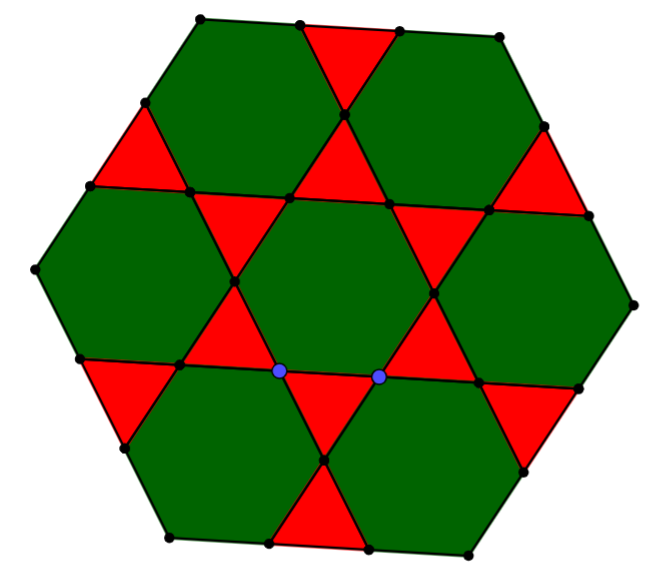
- Hexagons & Triangles (but a different pattern)
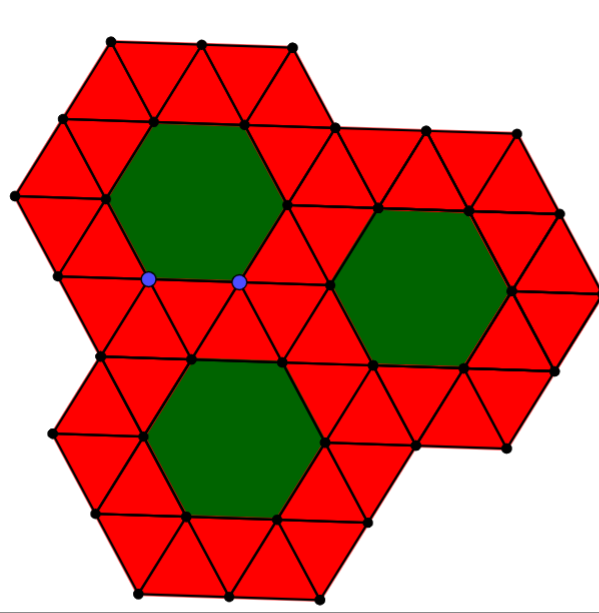
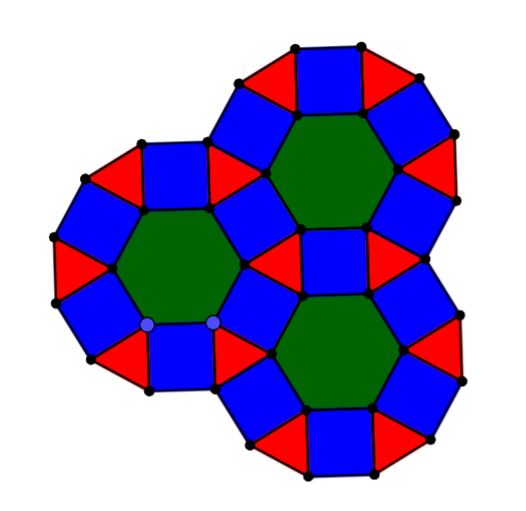
- Hexagons & Triangles & Squares
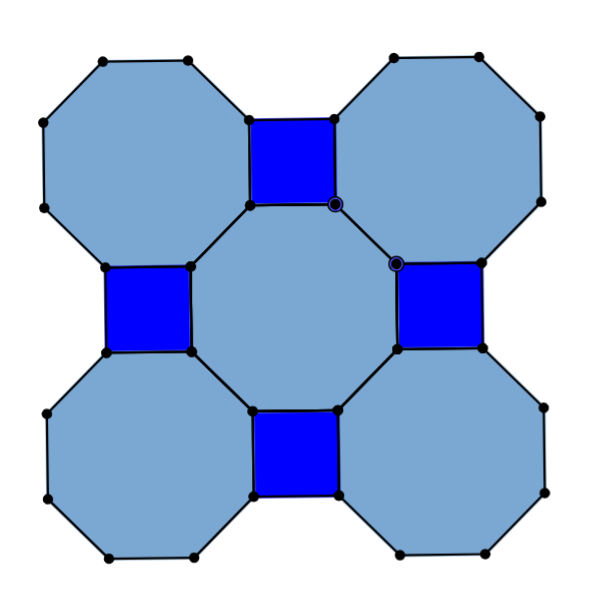
- Octagons & Squares
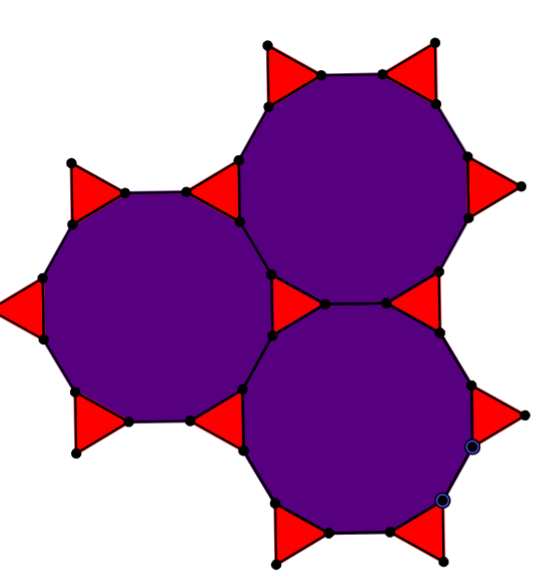
- Dodecagons & Triangles
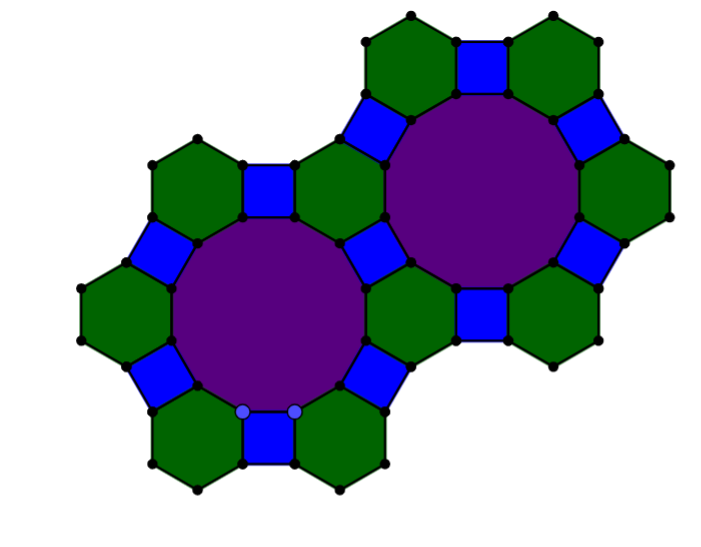
- Dodecagons & Squares & Hexagons
See this article for more on the notation introduced in the problem, of listing the polygons which meet at each point.
You may also like
Triominoes
A triomino is a flat L shape made from 3 square tiles. A chess board is marked into squares the same size as the tiles and just one square, anywhere on the board, is coloured red. Can you cover the board with trionimoes so that only the square is exposed?
LOGO Challenge 5 - Patch
Using LOGO, can you construct elegant procedures that will draw this family of 'floor coverings'?
LOGO Challenge - Triangles-squares-stars
Can you recreate these designs? What are the basic units? What movement is required between each unit? Some elegant use of procedures will help - variables not essential.