Get Cross

'Get Cross' printed from https://nrich.maths.org/

Show menu

Congratulations for your solutions to Hyeyoun Chung, age 17, St Paul's Girls' School, London; Royce Ferguson; Ang Zhi Ping, age 16; Yatir Halevi, age 17, Maccabim and Reut High-School, Israel; and Joe Nielson, Rowan Maclennon-Ryde and Elizabeth Brewster from Madras College, St Andrew's, Scotland.

The radius of the circle OA can be found by using the right triangle formed by $AB = (1 + (\sqrt 2)/2)$ and $BO = (\sqrt 2)/2)$. Using Pythagoras' theorem, the radius is found to be $OA = \sqrt(2 +\sqrt 2)$ units and the area of the circle to be $\pi (2 + \sqrt 2)$.

Now, connect the centre of the circle to the 8 points on it's circumference where the white meets red. This divides the white into circular sectors and quadrilaterals.

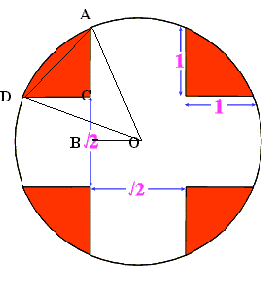
Diagram.

Using the cosine rule to find $\angle AOD$ we have $AC=CD=1$ and so $AD = \sqrt 2$ and hence

$$\cos \angle AOD = {{OA^2 + OD^2 -AD^2}\over 2OA.OD} = {1 \over \sqrt 2}.$$

Hence $\angle AOD = 45$ degrees.

The area of the triangle $AOD$ is

$${1\over 2} OA \times OD \times \sin \angle AOD = {\sqrt 2 \over 4}(2 + \sqrt 2).$$

To find the area of the minor segment $AD$ we subtract the area of triangle $AOD$ from the area of sector $AOD$ which gives

$${\pi \over 8}(2 + \sqrt 2) - {\sqrt 2 \over 4}(2 + \sqrt 2).$$

To get the total red shaded area we now add the area of triangle $ACD$ and multiply by $4$ which gives:

$$4[{\pi \over 8}(2 + \sqrt 2) - {\sqrt 2 \over 4}(2 + \sqrt 2)+ {1\over 2}]={\pi \over 2}(2 + \sqrt 2)- 2\sqrt 2 \approx 2.535 \rm {\ sq. \ units} .$$