Copyright © University of Cambridge. All rights reserved.
'Sangaku' printed from https://nrich.maths.org/
Show menu
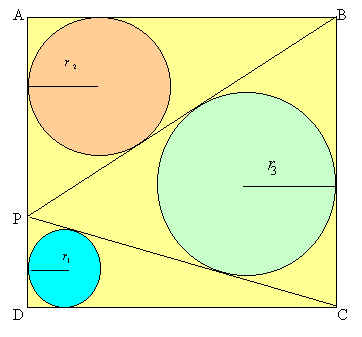
The square $ABCD$ has sides of length 1 unit and it is split into three triangles by the lines $BP$ and $CP$. If $P$ is the midpoint of $AD$, find the radii of the inscribed circles of these triangles.
Now suppose the lengths $AP$ and $PD$ are $(1- p)$ and $p$ respectively. Find the radii of the three circles $r_1$, $r_2$and $r_3$ in terms of $p$ and plot, on the same axes, the graphs of $r_1$, $r_2$ and $r_3$ as $p$ varies from 0 to 1. Can the ratio of the radii $r_1 : r_2 : r_3$ ever take the value $1:2:3$?
Notes and Background
Sangaku in Japanese means a mathematics tablet. During the Edo period (1603-1867) when Japan was cut off from the western world, people of all classes produced theorems in Euclidean geometry as beautifully coloured drawings on wooden tablets to be hung in a temple. Proofs were rarely given. The tablets challenged other geometers: "See if you can prove this."
Sangaku in Japanese means a mathematics tablet. During the Edo period (1603-1867) when Japan was cut off from the western world, people of all classes produced theorems in Euclidean geometry as beautifully coloured drawings on wooden tablets to be hung in a temple. Proofs were rarely given. The tablets challenged other geometers: "See if you can prove this."