Reyna from Downside School, Jian from NLCS Jeju in South Korea and Kian from King Edward VII School in the UK all found the area of the quadrilateral using ratios. They all used the result below, which Kian and Jian both proved. This is Jian's proof:
 

Jian, Kian and Reyna used this idea to find the area of the quadrilateral. This is Reyna's working:
 

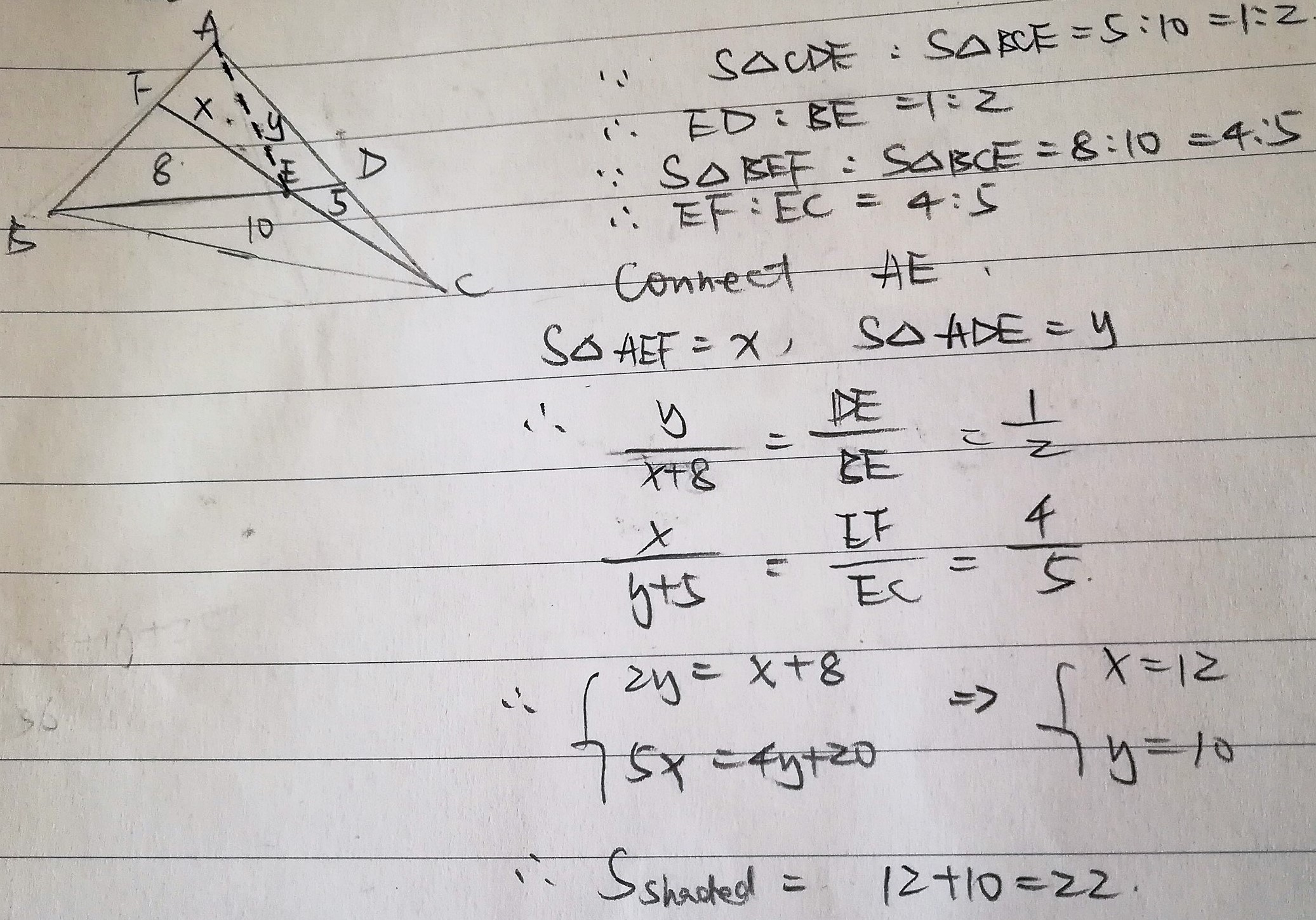
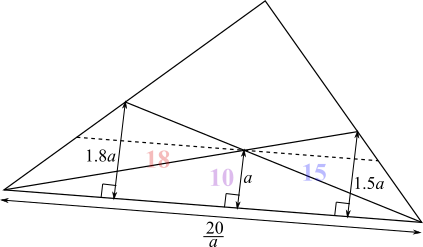 Jack used a different method:
The problem is best solved considering the similar triangles made from drawing a line parallel to the base through the cross of the two diagonals.

I found the ratio of the heights of the combined triangles of area $15$ and $18$ and the triangle of area $10.$

Then Jack used the fact that the triangles on the line parallel to the base are similar to those on the base, so their areas can be found by multiplying by the squares of the scale factors:
 
$\left(\dfrac{0.8}{1.8}\right)^2\times18=\dfrac{6.4}{1.8}=\dfrac{32}9$

$  \left(\dfrac{0.5}{1.5}\right)^2\times15=\dfrac{15}{9}=\dfrac{5}3$

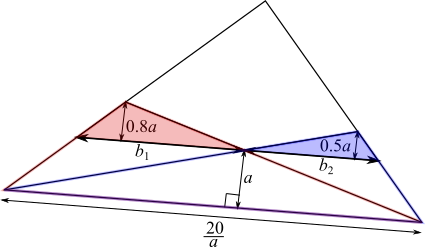
$\dfrac{32}9=\dfrac120.8ab_1\Rightarrow b_1=\dfrac{80}{9a}$

$\dfrac{5}3=\dfrac120.8ab_2\Rightarrow b_2=\dfrac{20}{3a}=\dfrac{60}{9a}$

After solving for their area I was able to find the width of the triangle at that height
($b_1+b_2$) and used ratios to find the height of the triangle.
$b_1+b_2=\dfrac{140}{9a}$
$h=4.5a$ (going up $a$ units along the height, the base gets shorter by $\frac{40}{9a}$ units. The base is $\dfrac{20}a$, and $\dfrac{20}a\div\dfrac{40}{9a}=4.5$. So after going up $a$ units $4.5$ times, the 'base' has reached $0$ - so we are at the point of the triangle)

I then obtained an area of $45-23=22$ for the quadrilateral.