 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Days and Dates



Days and Dates printable worksheet
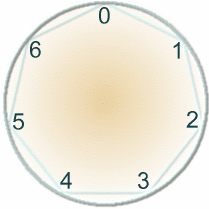
If today is Monday we know that in 702 days' time (that is in 100 weeks and 2 days' time) it will be Wednesday. This is an example of "clock" or "modular" arithmetic.
What day will it be in 15 days? 26 days? 234 days?
In 2, 9, 16 and 23 days from now, it will be a Wednesday.
What other numbers of days from now will be Wednesdays?
Can you generalise what you have noticed?
Choose a pair of numbers and find the remainders when you divide by 7.
Then find the remainder when you divide the total by 7. For example:
| $15 \div 7 = 2$ remainder $1$ | $15 + 26 = 41$ | |
| $26 \div 7 = 3$ remainder $5$ | $41 \div 7 = 5$ remainder $6$ |
Choose some more pairs of numbers.
Is there a relationship between the remainders when you divide each by 7, and the remainder when you divide their total by 7?
Now find the remainder when you divide the product of 15 and 26 by 7. What happens?
Choose some more pairs of numbers.
Is there a relationship between the remainders when you divide each by 7, and the remainder when you divide their product by 7?
What about when you divide by numbers other than 7?
Can you explain what you've noticed?