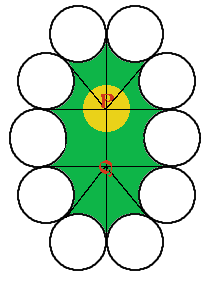
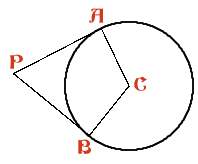
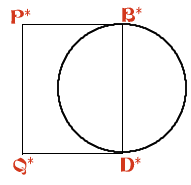
This model holly leaf is made in sections and joined together. Like a real holly leaf, it will not lie flat. It has negative curvature.

To make the holly leaf, a circle centre $C$ of radius 5 cm and radii $CA$ and $CB$ with $\angle ACB = 125$ degrees are drawn. The tangents to the circle at $A$ and $B$ meet at the point $P$. Eight identical 3 sided shapes are made by cutting along $PA$ and $PB$ and around the arc $AB$ to make a 3 sided shape with 2 straight edges and one edge along the minor arc of the circle (the circles are thrown away).

Two identical 4-sided shapes are made by drawing a circle with radius 5 cm, a diameter $B$*$D$* and tangents $B$*$P$* and $D$*$Q$*equal in length to $PB$. These shapes have edges $B$*$P$*, $P$*$Q$*, $Q$*$D$* and the semicircular arc (inside the rectangle) from $B$* to $D$*.

The sketch shows (on a smaller scale) how the ten pieces are joined together to make the "holly leaf".

Find the length of the boundary of the yellow area around $P$ which is bounded by six arcs centred at $P$, each of radius $r$ cm. All points on the boundary of the yellow region are equidistant from the point $P$.

If the surface at $P$ were flat, the boundary of the region would be a circle and its length would be $2\pi r$. In this case the length of the boundary is greater than $2\pi r$ and the surface of the "holly leaf" has negative curvature at $P$.

Compare the perimeter and area of this "holly leaf" with the similar flat leaf for which $\angle ACB = 135$ degrees.

See the problem "Holly" for the flat version of this problem.

What happens to the holly leaves as the angle $\angle ACB$changes?

[For positive curvature the boundary is less than $2 \pi r$ in length.]