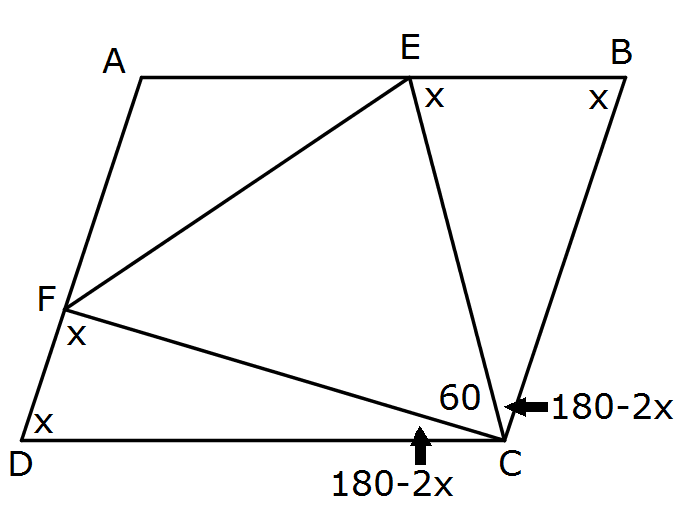
Triangle $DFC$ is isosceles $(CF=CD)$.

Hence $\angle DFC = \angle FDC = x^{\circ}$.

Hence $\angle FCD = (180-2x)^{\circ}$ (angle sum of triangle).

Now $\angle EBC = \angle FDC = x^{\circ}$ (opposite angles of a parallelogram) and triangle EBC is isosceles (CE = CB). Hence $\angle BEC = x^{\circ}$ and $\angle ECB = (180-2x)^{\circ}$

Lines $AD$ and $BC$ are parallel and hence $$\angle ADC + \angle BCD = 180^{\circ}$$ Therefore: $$x+2(180-2x) + 60= 180$$i.e.$420-3x=180$ i.e. $3x=240$ i.e. $x=80$