 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Subtended Angles



This problem has now been superseded by Circumference Angles
In this problem you can make use of the interactivity below.
Choose two points on the edge of the circle. Call them $A$ and $B$.
Join these points to the centre, $C$. What is the angle at $C$?
Join $A$ and $B$ to a point on the edge. Call that point $D$. What is the angle at $D$?
What do you notice?
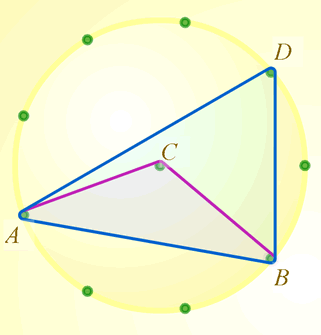
Would the same thing happen if $D$ took a different position on the edge of the circle?
Would the same thing happen if you started with a different two points on the edge of the circle?
Would the same thing happen if you started with any two points on the edge of any circle?
Can you prove it?
For printable sets of circle templates for use with this activity, please see Printable Resources page.
Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geo-board.
The boards, moulded in crystal clear ABS that can be used on an OHP (185 cm in diameter), together with a teacher's guide, are available from Geoff at Education Initiatives