Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Subtended Angles
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Arun from the National Public School in Bangalore sent us this detailed solution:
It is clearly seen that the angle at $C$ is twice the angle at $D$. Here we have the fundamental theorem with regard to angles in circles -" the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the circle "
This can be proved as follows :
Given a circle $(C,r)$ in which arc $AB$ subtends angle ($ACB$) at the centre and angle ($ADB$) at any point $D$ on the circle.
To Prove:
(i) angle $(ACB)$ = $2\times$angle $(ADB)$, when arc $AB$ is a minor arc or a semicircle.
(ii) Reflex angle $(ACB) = 2\times$ angle $(ADB)$, when arc $AB$ is a major arc
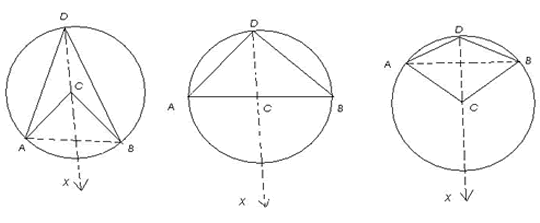
Construction: Join $AB$ and $DC$. Produce $DC$ to a point $X$ outside the circle.
Clearly, there are 3 cases.
Case I : arc $AB$ is a minor arc [Fig (i)]
Case II : arc $AB$ is a semicircle [Fig (ii)]
Case III : arc $AB$ is a major arc [Fig (iii)]
We know that when one side of a triangle is produced then the exterior angle so formed is equal to the sum of the interior opposite angles.
Therefore,
angle $(ACX)$ = angle $(CAD)$ + angle $(CDA)$ [consider triangle $CAD$]
angle $(BCX)$ = angle $(CBD)$ + angle $(CDB)$ [consider triangle $CBD$]
But,
angle $(CAD)$ = angle $(CDA)$ [since $CD = CA = r$ ] and ,
angle $(CBD)$ = angle $(CDB)$ [since $CD = CB = r$ ]
Therefore,
angle $(ACX) = 2\times$ angle $(CDA)$ and
angle $(BCX) = 2\times$angle $(CDB)$
In Fig (i) and Fig (ii) ,
angle $(ACX)$ + angle $(BCX)$ = $2 \times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
angle $(ACB)$ = $2 \times$angle $(ADB)$
in Fig (iii),
angle $(ACX)$ + angle $(BCX)$ = $2\times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
reflex angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
reflex angle $(ACB)$ = $2\times $ angle $(ADB)$
Hence proved.
This theorem has 2 main implications:
(i) The angle in a semicircle is a right angle .
i.e. in fig (2), where arc $AB$ is a semicircle, or in other words $ACB$ is a diameter,
angle $(ADB) = \frac{1}{2} \times$ angle $(ACB) = \frac{1}{2}\times$($180$ degrees) = $90$ degrees = a right angle
This holds true for any position of point $C$ on the semicircle.
(ii) Angles in the same segment of a circle are equal.
This means that if an arc subtends $2$ angles, at $2$ different points on the circle, these angles will be equal.
We can prove this, by proving that each of the $2$ angles is equal to half the angle subtended at the centre.
You may also like
On Time
On a clock the three hands - the second, minute and hour hands - are on the same axis. How often in a 24 hour day will the second hand be parallel to either of the two other hands?
LOGO Challenge 1 - Star Square
Can you use LOGO to create this star pattern made from squares. Only basic LOGO knowledge needed.