This problem follows on from Total Totality.

This network has nine edges which meet at six nodes. The numbers $1, 2, 3, 4, 5, 6$ are placed at the nodes, with a different number at each node. Is it possible to do this so that the sum of the two numbers at the ends of an edge is different for each edge?
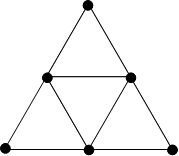
Either show a way of doing this, or prove that it is impossible.
 
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.