Rosalind Goudie from Madras College, St Andrew's sent a good solution to this problem.

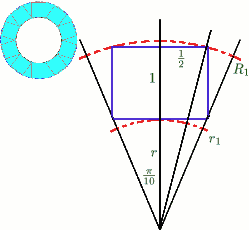
Consider the `necklace' with inner and outer radii $r_1$ and $R_1$. We divide the circle up into ten equal sectors as shown in the diagram. Then $r_1 = {\textstyle {1 \over 2}}\cot ({\pi \over 10})$ and, by Pythagoras' Theorem, $$R_1^2 = (r_1+1)^2+({1 \over 2})^2.$$ Thus, for the `necklace', $r_1= 1.539$ and $R_1= 2.588$.

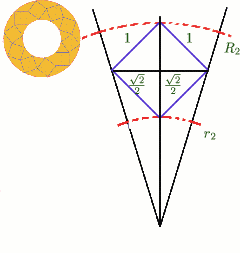
Consider the `floret' with inner and outer radii $r_2$ and $R_2$. Again we divide the circle up into ten equal sectors as shown in the diagram. Then $R_2 = r_2 +\sqrt{2}$, and $$\tan {\pi\over 10} = {\sqrt{2}/2\over \sqrt{2}/2 + r_2} = {1\over 1+r_2\sqrt{2}}.$$ Thus, for the `floret',$r_2 = 1.469$ and $R_2 = 2.883$. Hence the annulus containing the necklace lies inside the annulus of the floret.