Copyright © University of Cambridge. All rights reserved.
'Triangles Within Triangles' printed from https://nrich.maths.org/
Show menu
This diagram shows how the first
triangular number can be added to 3 copies of the second triangular
number to make the fourth triangular number:
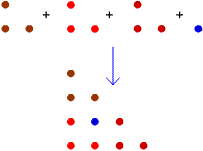
That is: $$ T_1 + 3 \times T_2 = T_4 $$ Here is a diagram showing how the second and third triangular numbers can be combined to make the sixth triangular number:
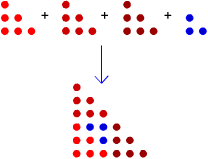
$$ T_2 + 3 \times T_3 = T_6 $$ Can you generalise this rule?
Can you find a rule in terms of $ T_n $ and $T_{n+1}$?