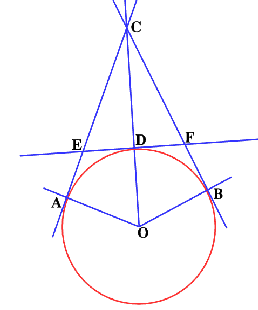This involves nothing more than areas of right angled triangles, using the symmetry in the diagram, and sines, cos's and tan's.

Well done M.S. Ezzeri Esa from Cambridge Tutors College, Croydon and thank you for this solution.

Let radius = $r$; $\angle AOD = \angle BOD = \alpha$

Area $ADBO$ = $2 ({1\over 2 }r^2 \sin \alpha) = r^2 \sin \alpha$

Area $ABO$ = ${1\over 2}r^2 \sin 2\alpha = r^2 \sin \alpha \cos \alpha$

Area $ACBO$ = $2({1\over 2}r^2 \tan \alpha) = r^2 \tan \alpha$

(Area $ABO$). (Area $ACBO$) = $r^2 \sin \alpha \cos \alpha\ .\ r^2 \tan \alpha = r^4 \sin^2 \alpha ={\rm (Area ADBO)}^2.$

The area of $ADBO$ is the geometric mean of the areas of $ABO$ and $ACBO$