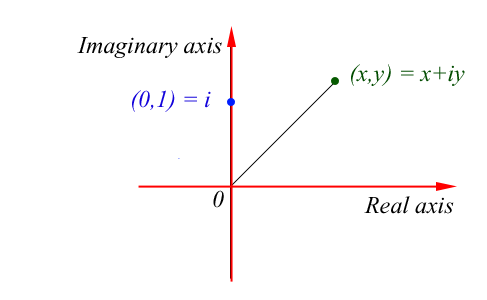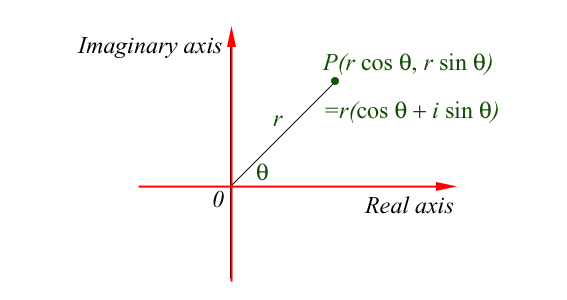Copyright © University of Cambridge. All rights reserved.
The Argand Diagram
In introducing complex numbers, and the notation for them, this article brings together into one bigger 'picture' some closely related elementary ideas like vectors and the exponential and trigonometric functions and their derivatives.
The real numbers are represented by the points on the real line (the $x-$axis) and the complex numbers by the points in the Euclidean plane. To each complex number there is associated a point in the plane with coordinates given by an ordered pair $(x,y)$ of real numbers $x$ and $y$.
We denote the point $(x,y)$ by a new symbol $x+iy$ where $i^2=-1$ and combine these objects according to the ordinary rules of algebra. We identify the real number $x$ with the point $(x,0)$ and the complex number $x+0i$ also with the point $(x,0)$ so we see that the real numbers are in fact a subset of the complex numbers. In a similar way we identify the complex number $i$ with the point
$(0,1)$.
The Arithmetic of Complex Numbers
Before we are happy that these 'objects' are called numbers we must see that it is possible to add, subtract, multiply and divide them and that they obey the rules of elementary algebra.
If $x_1$, $y_1$, $x_2$, and $y_2$ are any real numbers then, using the fact that $i^2=-1$, we can can add, subtract and multiply complex numbers as follows: \begin{eqnarray} (x_1 + i y_1) + (x_2 + i y_2) &=& (x_1 + x_2) +i(y_1 + y_2) \\ (x_1 + i y_1) - (x_2 + i y_2) &=& (x_1 - x_2) +i(y_1 - y_2)\\ (x_1 + i y_1)(x_2 + i y_2) &=& (x_1 x_2 + i^2 y_1 y_2) + i(x_1 y_2 +
x_2 y_1)\\ &=& (x_1 x_2 - y_1 y_2) + i(x_1 y_2 + x_2 y_1) \end{eqnarray}
The rule for division uses the fact that $(x+i y)(x-i y)=x^2+y^2$ so, provided that $x_2$ and $y_2$ are not both zero, we can divide by $x_2 +i y_2$ as follows: $$ {{x_1+i y_1} \over {x_2+i y_2}} = {{(x_1+i y_1)(x_2-i y_2)}\over {(x_2+i y_2)(x_2-i y_2)}}= {{(x_1 x_2+y_1 y_2)+i(x_2 y_1-x_1 y_2)}\over x_2^2+y_2^2}$$ which is again of the form [real number + $i\times$real number]. For example
$${{3+i}\over {1+2i}} = {{(3+i)(1-2i)}\over 5} = {5-5i \over 5} = 1-i.$$
Complex Numbers as Vectors
The rules for adding and subtracting complex numbers, namely to add or subtract corresponding components, are exactly the same as the rules for adding and subtracting vectors. Complex numbers behave exactly like two dimensional vectors. Indeed real numbers are one dimensional vectors (on a line) and complex numbers are two dimensional vectors (in a plane).
The natural question to ask is 'could there be three dimensional numbers corresponding to three dimensional vectors or could there even be higher dimensional numbers?'. The answer is no. The only sets of numbers which satisfy all the usual rules of elementary algebra (that is satisfy the field axioms) have dimension one or two. We can define division of complex numbers but we cannot define
division of three dimensional vectors. There are no three dimensional or higher dimensional numbers obeying all the rules of elementary algebra. While there are four dimensional numbers, called quaternions, multiplication of them is not commutative, that is, for some quaternions $p$ and $q$ we have $p q \neq q p$.
Complex Numbers and Solutions of Polynomial Equations
Once we know about complex numbers, immediately we see that quadratic equations like $x^2+2x+5=0$ have solutions $${-2\pm \sqrt -16 \over 2}= -1\pm 2i.$$ What is more it is possible to prove the beautiful Fundamental Theorem of Algebra which states that not only do quadratic equations always have two roots, and cubic equations always have three roots, but every polynomial equation of degree
$n$ has exactly $n$ roots.
The Modulus and Argument of a Complex Number
In defining the trigonometric functions $\sin \theta$ and $\cos \theta$ we associate the values of these functions with the coordinates of points on the unit circle (the circle of radius one unit and centre the origin). On this circle, if $P$ is the point such that the angle between the $x-$axis and $O P$ (measured in a counter-clockwise direction) is $\theta$, then the coordinates of $P$
are given by $x=\cos \theta$ and $y=\sin \theta$. When the ray $O P$ has rotated through an angle of 360 degrees or $2\pi$ radians it retraces the same path and repeats the same values of $\cos \theta$ and $\sin \theta$ showing that these functions are periodic with period $2\pi$.
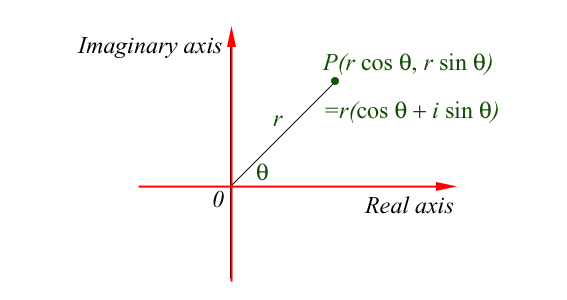
Now there is a connection between the complex number $z=x + i y$ and the trigonometric functions. If the point $P$ corresponding to the complex number $z$ lies on the circle with radius $r$, where the angle between the $x$-axis and the ray $O P$ is $\theta$, then $O P^2 = r^2 = x^2 + y^2$ and $z = r(\cos \theta + i \sin \theta)$. The length $O P$, equal to $\sqrt(x^2+y^2)$, is called the
modulus of the complex number $z$ and it is denoted by $|z|$. The angle $\theta$ between $O P$ and the $x$-axis, measured in a counter-clockwise direction, is called the argument of the complex number.
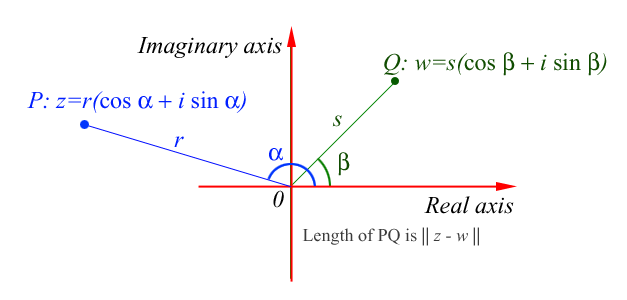
The distance between two points in the plane $P$ and $Q$ corresponding to the complex numbers $z_1=(x_1,y_1)$ and $z_2=(x_2,y_2)$ is given by the modulus of the vector ${\bf \it P Q} $ which is the same as the modulus of the complex number $z_1 - z_2$, namely: $$|z_1 - z_2| = \sqrt((x_1-x_2)^2 + (y_1-y_2)^2)$$.
If two points $P$ and $Q$ are equidistant from the origin, that is if they both lie on a circle of radius $r$ with the origin as its centre, then the length of the arc of this circle between $P$ and $Q$ is given by $r$ times the difference in their arguments measured in radians.
Complex Numbers and Transformations in The Plane
 |
Functions of a complex variable provide an efficient way to work mathematically with transformations in the plane.
Isometries are transformations that preserve angles and distances. Reflections, translations, rotations and glide reflections are isometries. All the isometries are combinations of reflections. For an introduction to this idea see Mirror Mirror and . ..on The Wall.
To follow up the idea that all the isometries are combinations of reflections, and to see how functions of a complex variable are used to work with transformations, see Footprints. |
Some of the History of Complex Numbers
Historically these numbers were thought of simply as mathematical tools useful in solving equations and called imaginary numbers . We call $x$ the real part and $y$ the imaginary part of the complex number and these terms were introduced by Descartes (1596 - 1650) whose
name gave rise to the term Cartesian coordinates. These so-called 'numbers' were treated with much suspicion by mathematicians for around another 200 years or so. Wallis (1616 - 1703) realised that real numbers could be represented on a line and made an early attempt to represent complex numbers as points in the plane. Then Wessel (1797), Gauss (1800) and Argand (1806) all successfully
represented complex numbers as points in the plane. Gauss introduced the name complex numbers in 1832. In the nineteenth century Cauchy, Riemann and other mathematicians incorporated complex numbers into analysis thus extending the analysis of real numbers and giving complex numbers equal status.
The most important mathematical constants in one formula
We shall now explain the result $$\cos \theta + i\sin \theta = e^{i\theta} = \exp(i\theta)$$ proved by Euler in 1748, which leads to the very striking formula $$e^{i\pi} = -1.$$
We assume that the reader is familiar with the fact that the derivative of $\sin \theta$ with respect to $\theta$ is $\cos \theta$ and the derivative of $\cos \theta$ is $-\sin \theta$. Hence the derivative of $\cos \theta + i\sin \theta$ is $$-\sin \theta + i\cos \theta = i(\cos \theta + i \sin \theta)$$ so that $f(\theta)= \cos \theta + i \sin \theta$ satisfies the differential equation
$${\mathrm{d}f(\theta) \over \mathrm{d\theta}} = {i}f(\theta).\quad (1)$$ The exponential function is the function $g(x) = \exp(x)$ which satisfies the differential equation $${\mathrm{d}g(x)\over \mathrm{dx}} = g(x).$$ It follows that if $g(\theta) = \exp(i\theta)$ then $${dg(\theta) \over \mathrm{d\theta}} = i g(\theta).\quad (2)$$ but this is exactly the same differential equation as equation
(1) so the functions $f$ and $g$ can only differ by a constant as they have the same derivative. Putting $\theta = 0$ we see that $f(0)=g(0)=1$ so these two functions must in fact be identical. This proves that $\cos \theta + i \sin \theta = \exp(i\theta)$. Then putting $\theta$ equal to $\pi$ we have $\cos \pi = -1$ and $\sin \pi = 0$, thus $$e^{i\pi} = -1.$$ This proof uses differential
equations and it is not just an exercise in solving them.