Copyright © University of Cambridge. All rights reserved.
'Andy's Marbles' printed from https://nrich.maths.org/
Several very well reasoned solutions came in for this problem about Andy's marbles. Katherine from Treffos, North Wales, pupils from Wigginton Primary and Stephen from Frisby School all went about the problem in a similar way. Stephen said:
I know that to solve this problem I have to work backwards, beginning with the last part, and ending with the first.
So... Andy walks away with 14 marbles, 2/3 of what was recovered. His friend walks away with 1/3 of what was recovered. 14 is 2/3 so to find out 1/3 I then half 14, getting 7. Sam had 7 and Andy had 14. A total rescued of 14 + 7 = 21
21 is half (1/2) of what was lying around on the ground, the other half having been taken by the children. To find how many were on the ground nearby I have to double 21. I now have an answer of 42.
42 must be doubled to get the final answer, as 1/3 and 1/6 went down drains or hills (1/3 + 1/6 = 1/6 + 2/6 =1/2).
This gives me a final answer of 84 marbles in the bag.
To find out what fraction of the marbles Andy had given away or lost you have to find the fraction of marbles he was left with. He was left with 14 out of 84 marbles (14/84). You then work out the fraction in its lowest form. Firstly divide 14 and 84 by 2 to get 7/42 then divide them by 7 to get an answer of 1/6. However 1/6 is what he is left with so he must have lost or given away 5/6 of
his marbles!
Michael from King Henry VIII found a different method for solving the problem:
Andy has x marbles
1/6 go down the drain, and 1/3 roll down the slope
That comes to 3/6 or 1/2
x/2
1/2 the remaining 1/2 are stolen, leaving 1/4
x/4
He gave 1/3 to his friend, leaving 1/4*2/3 0r 2/12 or 1/6
x/6
That left 14
x/6=14
Times both sides by 6 and you get x=84
He had 84 marbles, and he had lost or given away 5/6
We also received two solutions from students at The British School of Brussels, both of whom used a bar modelling approach. Here is Monty's:
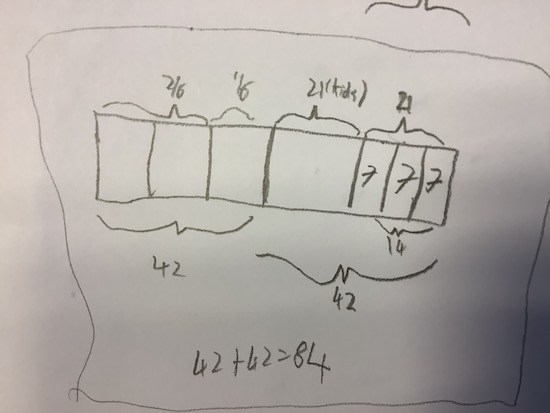
And here is Julia's:
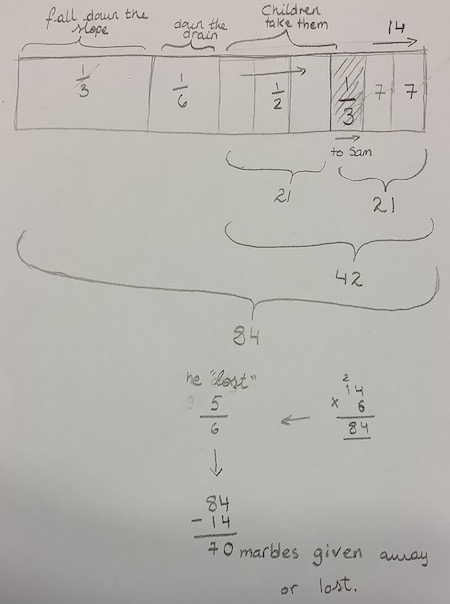
Can you see how they have used a bar to represent the total number of marbles that Andy had to begin with? Then they have split this 'whole' into parts according to the fractional amounts stated in the problem.
These are all very clear solutions, well done. Working from the end of a problem can be a useful way of tackling it - something to remember!

