Copyright © University of Cambridge. All rights reserved.
'Lunar Angles' printed from https://nrich.maths.org/
Show menu
Here is an excellent solution from Andrei from School No. 205,
Bucharest, Romania.
I divided the solution into two parts: the demonstration of the congruence of angles, and the demonstration that the three angles add up to $180^o$.
1. Congruence of angles in a lune
Let $O_1$ and $O_2$ be the centres of two circles, $A$ and $B$ the intersection points and $M$ and $N$ the intersections of the tangents to these two circles. I observed that triangles $O_1AO_2$ and $O_1BO_2$ are congruent, because they have a common side $O_1O_2$, and the other two sides are radii in the two circles. So, angle $O_1AO_2$ and $O_1BO_2$ are equal to say $\theta$. A tangent to a circle and the radius to the point of contact are perpendicular so $\angle MAO_2 = \angle NAO_1 =\angle MBO_2 = \angle NBO_1 = 90^o$. Hence $\angle O_1AM = \angle O_2AN =\angle O_1BM =\angle = \angle O_2BAN = \theta - 90^o$. So, $\angle MAN = \angle MBN$.
2. Let $O_1$, $O_2$ and $O_3$ be the centres of the three circles respectively, D the point common to all three circles, and $T_1T_1'$, $T_2T_2'$, $T_3T_3'$ the three tangents. In my figure the radius and the tangent to circle 1 are in red, to circle 2 in blue and to circle 3 in green respectively.
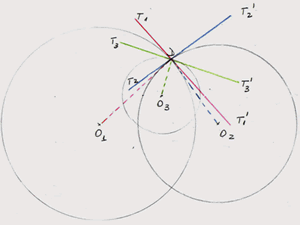
From the previous point, I see that angle $\alpha$ has the same measure with angle $T_2DT_1'$ and to the angle $T_1DT_2'$ (the last two being vertically opposite angles).
In the same manner I found: $\beta = \angle T_1'DT_3' =\angle T_1DT_3$ and $\gamma = \angle T_3DT_2 = \angle T_3'DT2'$. \par This way, it is easy to see that the three angles add up to $180^o$: $\alpha + \beta + \gamma = T_2DT_1' + T_1'DT_3' + T_3'DT_2' = T_2DT_2' = 180^o$. \par For the second case, I follow exactly the same steps.
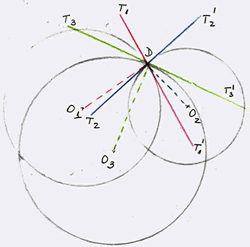
I find $\alpha = \angle T_2DT_1'$, $\beta = \angle T_2'DT_3' = \angle T_2DT_3$ and $\gamma \angle T_3DT_1 = \angle T_3'DT_1'$.
The result is the same, i.e. that in this case the three angles add up to $180^o$ again.
I divided the solution into two parts: the demonstration of the congruence of angles, and the demonstration that the three angles add up to $180^o$.
1. Congruence of angles in a lune
Let $O_1$ and $O_2$ be the centres of two circles, $A$ and $B$ the intersection points and $M$ and $N$ the intersections of the tangents to these two circles. I observed that triangles $O_1AO_2$ and $O_1BO_2$ are congruent, because they have a common side $O_1O_2$, and the other two sides are radii in the two circles. So, angle $O_1AO_2$ and $O_1BO_2$ are equal to say $\theta$. A tangent to a circle and the radius to the point of contact are perpendicular so $\angle MAO_2 = \angle NAO_1 =\angle MBO_2 = \angle NBO_1 = 90^o$. Hence $\angle O_1AM = \angle O_2AN =\angle O_1BM =\angle = \angle O_2BAN = \theta - 90^o$. So, $\angle MAN = \angle MBN$.
2. Let $O_1$, $O_2$ and $O_3$ be the centres of the three circles respectively, D the point common to all three circles, and $T_1T_1'$, $T_2T_2'$, $T_3T_3'$ the three tangents. In my figure the radius and the tangent to circle 1 are in red, to circle 2 in blue and to circle 3 in green respectively.

From the previous point, I see that angle $\alpha$ has the same measure with angle $T_2DT_1'$ and to the angle $T_1DT_2'$ (the last two being vertically opposite angles).
In the same manner I found: $\beta = \angle T_1'DT_3' =\angle T_1DT_3$ and $\gamma = \angle T_3DT_2 = \angle T_3'DT2'$. \par This way, it is easy to see that the three angles add up to $180^o$: $\alpha + \beta + \gamma = T_2DT_1' + T_1'DT_3' + T_3'DT_2' = T_2DT_2' = 180^o$. \par For the second case, I follow exactly the same steps.

I find $\alpha = \angle T_2DT_1'$, $\beta = \angle T_2'DT_3' = \angle T_2DT_3$ and $\gamma \angle T_3DT_1 = \angle T_3'DT_1'$.
The result is the same, i.e. that in this case the three angles add up to $180^o$ again.