I've been playing around exploring what sort of shapes you can make with cubes. I particularly like those cubes that link together like Multilink ©. I'm sure that many of you have come across them or something similar.You can make all kinds of designs, perhaps pretending that you are making an animal or an alien or designing a house or some futuristic building or in fact, you can just imagine that you are creating rather interesting shapes and are happy with that.It is quite a good idea to set some sort of rule or rules that you have to follow and see how many models/designs you can make if you follow those rules.

I think a good challenge to start with is;
 

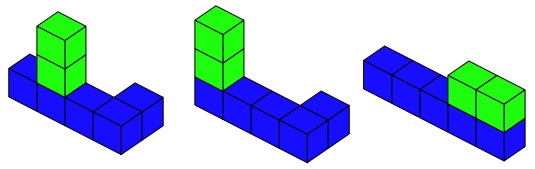
Use 7 of these cubes - 5 of them of one colour and 2 of another colour. These 7 have all to be joined together.

Now let's say that the cubes have to be joined "properly", that is with no twists, so a that a square face is flat against the next square face.So the two main rules that will control how we will build are as follows:-

The five that are of one colour must all touch the table that you are working on.

The two that are of a different colour must NOT touch the table.

Well, I wonder how many different designs you can discover or forecast?

Unless you have lots and lots, I really mean lots, of these cubes to use you will have to make a record of what you have done each time. This can be useful so that you can check that you have not done the same ones twice.
When you've done a few it would be good to see if there is a "system", or "particular way of working" that you are using or could use to make things easier.