Cube Roots

'Cube Roots' printed from https://nrich.maths.org/

Show menu

We have to find values of c - d where:

$\begin{eqnarray} c & = &{(5\sqrt{2}+7)}^{\frac{1}{3}} \\ d & = &{(5\sqrt{2}-7)}^{\frac{1}{3}} \end{eqnarray}$

Looking first for real roots, note that

$ (5\sqrt{2}+7)(5\sqrt{2}-7) = 50-49 = 1 $ so $c^3d^3=1 $ and hence $cd=1$ .

Also

$c^3-d^3=14$ giving

$\begin{eqnarray} (c-d)^3 & = & c^3 - d^3 - 3cd(c-d) \\ & = & 14-3(c-3) \end{eqnarray}$

$c-d$ satisfies $x^3+3x-14=0,$ and this has only one real root $x=2$ . \[ x^3+3x-14 = (x-2)(x^2+2x+7) = 0 \] . $x^2+2x+7=0$ has complex roots $-1+i\sqrt{6}$ and $-1-i\sqrt{6}$ .

Hence

$x=c-d=2$ is the only real value of the given expression.

There will be altogether 9 complex values of

$c-d$ because c can take 3 values and d can take 3 values. Denoting the cube roots of unity by 1, $\omega$ and $\omega^2$ , where $\omega = \cos{2\pi/3} + i \sin{2\pi/3} $ , the nine required values are given by: $2, 2\omega, \omega^2, (-1+ i\sqrt{6}), (-1+i\sqrt{6})\omega, (-1+i\sqrt{6})\omega^2, (-1-i\sqrt{6}), (-1-i\sqrt{6})\omega, (-1-i\sqrt{6})\omega^2 $

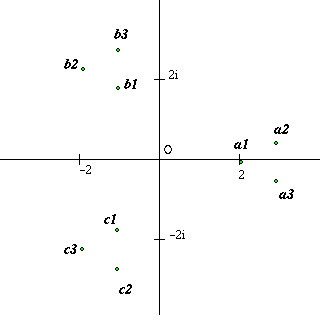$(5\sqrt{2}+7)^\frac{1}{3} - (5\sqrt{2} - 7)^{\frac{1}{3}}$
$\begin{eqnarray} b_1& =& 2\omega \\ b_2& =& (-1-i\sqrt{6})\omega^2 \\ b_3 & = & (-1+i\sqrt{6}) \\ c_1& = & 2\omega^2 \\ c_2 & = & (-1-i\sqrt{6}) \\ c_3 & = & (-1+i\sqrt{6}) \end{eqnarray}$

Neil of Madras College found the complex values and dicovered some beautiful patterns when he plotted them in the complex plane. Neil's discoveries can be generalised to a ^1/3 - b ^1/3 for any real or complex numbers a and b, and from cube roots to n th . roots.

In order to find patterns similar to the ones discovered by Neil, but in a simpler situation, and to see how his ideas can be generalised, you may like to plot the twelve values of 8 ^1/3 + 81 ^1/4 in the complex plane.