Chord

'Chord' printed from https://nrich.maths.org/

Show menu

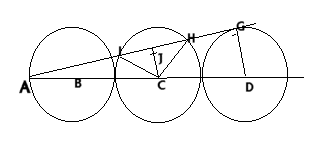Congratulations to four students from Madras College, Gordon and Alan from S6, Sue Liu from S4 and David from S3. They all sent excellent solutions to this problem including complete proofs of the general case. Answers also arrived from St Peter's College in Adelaide, Australia.

This is David's proof of the first part: Lines $CH$ and $CI$ can be drawn in. Both have length $R$ or 2 cm.

$ICH$ is an isosceles triangle which can be split into two congruent right angled triangles by drawing line $CJ$, where $J$ is the midpoint of chord $IH$.

Triangle $AJC$ is similar to triangle $AGD$, with a ratio of 6 cm to 10 cm or 3:5.

Line $GD = R= $2 cm,

Line $CJ =$ 3/5 $GD= $1.2 cm.

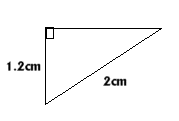Both right angled triangles $CJH$ and $CJI$ have lengths as below and the length $JH$ can be worked out using Pythagoras' theorem.

$JH^2 = 2^2 - 1.2^2 = 4 - 1.44 = 2.56 = 1.6^2$
So $JH = $1.6 cm and the chord $JH = $2(1.6)= 3.2 cm.

This is Gordon's proof of the general case of n circles where $AG$ cuts the m ^th circle at $I$ and $H$.

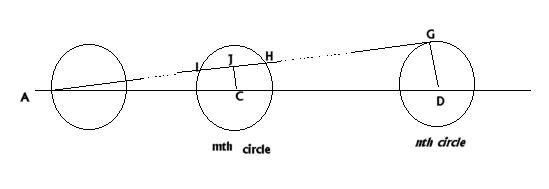
$\angle ACJ$ is similar to $\angle ADG$

$\Rightarrow AD = 2 \times2(n - 1) + 2 = 4n - 2$ units

$\Rightarrow AC = 4m - 2$ units.

$\eqalign{ \frac{JC}{AC} &= \frac{DG}{AD} \\ \frac{JC}{4m - 2} &= \frac{2}{4n - 2} \\ JC &= \frac{4m - 2}{2n - 1}}$

$\angle IHC$ is isosceles and $\angle CJI = \angle CJH = 90^{\circ}$.

Hence, by Pythagoras' theorem, $$IH = 2JH = 2\sqrt{2^2 - \left(\frac{4m - 2}{2n - 1}\right)^2}$$ Simplifying this expression gives $$IH = \frac{8}{2n - 1}\sqrt{n(n - 1) - m(m - 1)}$$ Checking this where $n=3$ and $m=2$ $$IH = \frac{8}{5}\sqrt{6 - 2} = \frac{16}{5} = 3.2$$