 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Smaller and Smaller



Here is an equilateral triangle which has sides of length 1 unit:
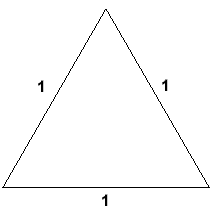
We could take out the middle third of each side and replace it with a spike. If the spike is made of two lines which are the same length as the missing section, it will look like this:
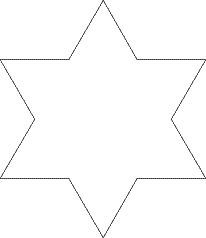
We could do the same again. Taking out the middle third of each line and replacing it with a spike in the same way gives this:
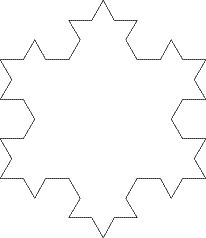
Remembering that the length of each side of our original equilateral triangle is 1 unit, what is the perimeter of the first shape we drew above? And the second? Can you see a pattern? Perhaps you can explain why this pattern comes about.
Can you predict, without drawing, what the perimeter of the next shape will be if we continue drawing them in the same way?
Could you predict the perimeter of any shape in the series?
The shapes above are called fractals. A fractal is made up of lots of copies of itself, each one smaller than the last. See also the problems Von Koch Curve, The Cantor Set and How Long is The Cantor Set?
You may also like
Chocolate
There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?
Tweedle Dum and Tweedle Dee
Two brothers were left some money, amounting to an exact number of pounds, to divide between them. DEE undertook the division. "But your heap is larger than mine!" cried DUM...