 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pick's Theorem



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
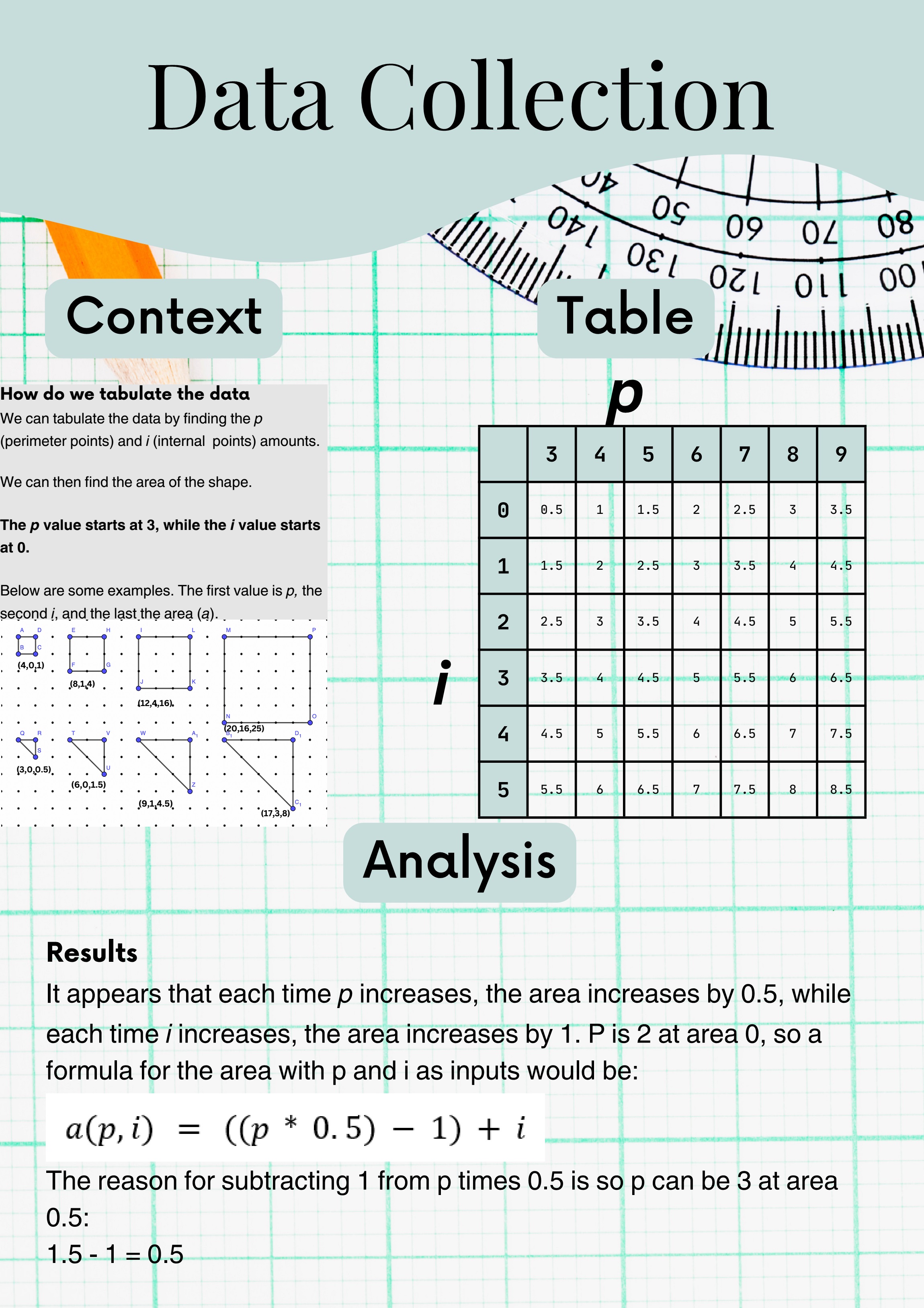
Aarav and Miranda from Brunswick South West primary school in Australia tried out different shapes. First they worked wth squares, then triangles, then rectangles. For each type of shape, they found some rules about its $p, i$ and $A.$ Click here to see ther work.
Their investigation is well-structured and they have derived great formulas, but it would be easier to link the results for the different shapes if they had used the same notation for each sequence – for example, finding all of the values of $p, i$ and $A$ in terms of each other, or the shortest sde of the shape.
Antonin and Winston from Parklane International School in Czech Republic worked very systematically, using lots of examples to look for patterns. Here is their work (click on the image to open a larger version):

 Note that there is actually another shape with $p=8$ and $i=1$ (shown left). Is its area the same as the one Antonin and Winston found?
Note that there is actually another shape with $p=8$ and $i=1$ (shown left). Is its area the same as the one Antonin and Winston found?
Are there any others? Could there be any with a different area?
Antonin and Winston continued their investigation (click on the image to see a larger version):
Pedro from Cambridge House Community College in Spain thought about why this formula works:
So the final relationship (formula) is:
Enclosed area = Internal dots + (Perimeter dots /2) - 1
By knowing 2 of them you can work the 3rd one out by rearranging the formula.
Explanation of each part of the formula:
1. Internal points: They are fully inside the polygon so are counted fully. They are needed in this formula as they tell us the polygon's shape more precisely and the amount of space inside it.
2. Perimeter points: Needed to know the lengths of the polygon (the total
perimeter).
3. You divide it by 2 as points on the boundary contribute to the perimeter of two edges. Dividing the total by 2 ensures that the contribution of these points to the area calculation is properly accounted for.
4. The -1 at the end is a correction factor as the very first perimeter point on the boundary (starting point) is counted twice, once for each of its adjacent edges. By subtracting 1, we avoid counting this point twice. With other words, so all lines are drawn you have to count it twice as it is counted at the start and at the end when joined from the other side.
Joshua shared a link to a video by the YouTuber "spacematt", which builds on Pedro's idea. You can watch the video here.