Copyright © University of Cambridge. All rights reserved.
'Colouring Triangles' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem will help children recognise reflective symmetry, but it offers more than that. By giving learners the freedom to create their own symmetrical patterns, they will push their own understanding of symmetry further and may well suprise you! It also provides an opportunity for children to discuss what
makes one symmetrical pattern different, or the same as, another. The task is designed with children's natural curiosity in mind - by hooking them in with the first images and the associated prompt of 'what can you see?', everyone can get started. The interactivity allows learners to pursue their curiosity by 'playing' with the ideas and this in turn provides consolidation of the
mathematics in a purposeful way.
Possible approach
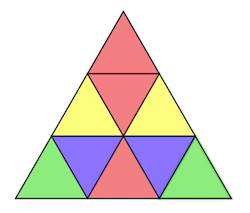
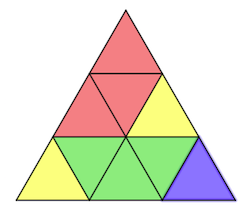
You could begin by displaying two sets of the triangles, each one coloured but only one of them a symmetrical design. (You may want to recreate the two pictures on this sheet, or display these images directly on the interactive whiteboard.) Invite the children to look carefully at the
images on their own for a moment, then talk to a partner about what they see.
Take suggestions from the class about what they notice. They may talk about the shapes they see, the colours, the number of colours, the number of triangles of each colour etc etc. Welcome all suggestions and if the idea of symmetry doesn't come up naturally, you may like to ask the group to look for differences between the two pictures.
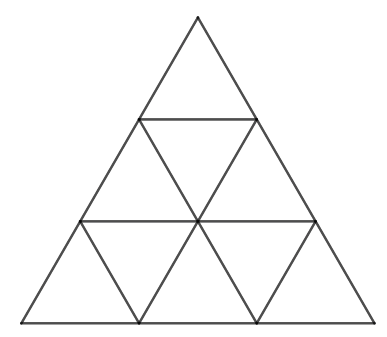
You can then set them off on the activity. Pairs would benefit from access to the interactivity on a computer, laptop or tablet as this allows them to try out ideas and easily tweak them. Having a copy of this sheet of the two coloured triangles to refer to, and this sheet of blank triangles to record their designs, would be helpful.
After a little while, give each pair time to share their designs with another pair so the four children together confirm that each way of colouring does indeed have line symmetry.
You can then set them off on the activity. Pairs would benefit from access to the interactivity on a computer, laptop or tablet as this allows them to try out ideas and easily tweak them. Having a copy of this sheet of the two coloured triangles to refer to, and this sheet of blank triangles to record their designs, would be helpful.
After a little while, give each pair time to share their designs with another pair so the four children together confirm that each way of colouring does indeed have line symmetry.
Let them work further on their designs and then encourage each pair to select just one to share with everyone at the end. (You could of course make an engaging display of these for the classroom wall.) The plenary can also be a time to bring up some points for discussion that might have arisen as the children worked. For example, did anyone create a design which had more than one line of
symmetry? If we turn the design round, does that make a new design or is it the same?
Key questions
Tell me about this design.
Where is the line of symmetry in this design?
Where is the line of symmetry in this design?
How do you know it is a line of symmetry?
Have you tried with fewer/more colours?
Possible extension
Encourage children to ask their own 'what if...?' questions. For example, what would happen if there were more triangles? What would happen if I was only allowed to colour in triangles on the bottom 'row'? What would happen if I joined two of the triangle designs together?
Alternatively, can learners colour the small triangles, using four colours, with no two triangles of the same colour side-by-side?
Alternatively, can learners colour the small triangles, using four colours, with no two triangles of the same colour side-by-side?
Possible support
Many children will be happier if they draw in the line of symmetry. You could also have mirrors available for those that want them. Some learners may want to cut out their triangles and try to fold them to check the mirror lines.