Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
LOGO Challenge 10 - Circles
Age 11 to 16
Challenge Level 





- Problem
- Teachers' Resources
These challenges arose from conversations and ideas during a Royal Institution Saturday morning Maths Workshop. Consider the procedure:
TO POLY :X :Y
REPEAT :Y [FD :X LT 360/:Y]
END
where :X and :Y are variables, that can be changed as you experiment and try to understand what is happening.
Think about, try to imagine, then experiment with:
POLY 50 7
POLY 20 16
POLY 20 30
etc..
What happens as the value for :Y increases yet further? (i.e. considering the limitations with your monitor's powers of resolution.)
.
.
.
BUT
.
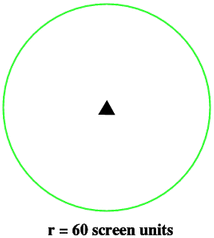
What is the most elegant way of coding the drawing of a circle of radius 60 screen units in the centre of your screen?
[Hint: use the primitive HOME to return turtle.]
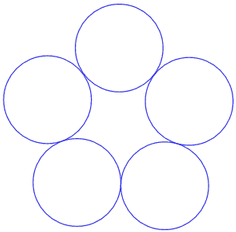
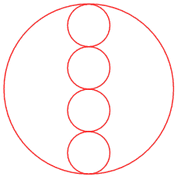
Naturally, geometric designs have long been embellished with circles.
You might like to consider re-creating the following designs this month.