 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2000 Revised 2006
Sperner's Lemma
If you try the Triangle Game you will probably soon suspect that it is not a fair game. Read on to find out the truth about it. Take a triangle ABC, labelled counterclockwise, and subdivide it into smaller triangles in whatever way you like. Then label all the new vertices as follows:
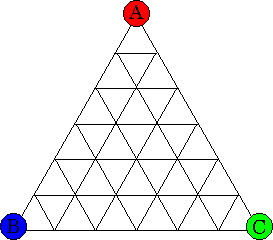
- vertices along AB may be labelled either A or B, but not C
- vertices along BC may be labelled either B or C, but not A
- vertices along CA may be labelled either C or A, but not B
- vertices inside triangle ABC may be labelled A or B or C.
Now shade in every small triangle in the subdivision that has three different labels.
Use two different shadings to distinguish the triangles which have been labelled counterclockwise (i.e. in the same sense as triangle ABC) from the triangles which have been labelled clockwise (i.e. in the sense opposite to that of as triangle ABC).
Then there will be exactly one more counterclockwise triangle than clockwise triangles. In particular, the number of shaded triangles will be odd.
This is Sperner's Lemma, named after its discoverer Emanuel Sperner, a 20th century German mathematician.
The term "lemma" may need explanation. It is used to describe a minor theorem which may not be of much interest in its own right, but plays an important role in some wider theory. Sperner's Lemma is a key result in topology. However, the result is so readily stated, and its proof is so accessible and elegant, that Sperner's Lemma should really be elevated to the status of a Theorem.
The proof of Sperner's Lemma requires no more than simple counting.
The proof starts by putting labels inside every small triangle. If the endpoints of the triangle are the same, the edge is labelled 0. If the vertices are different, and in the counterclockwise sense (the same sense as those of the outside triangle), label it 1. If the endpoints are different and in the clockwise sense (the opposite sense to that of the outside triangle, label it -1. Then add the three edge numbers and write the sum in a little circle in the middle of the triangle.
There are four possible outcomes:
- If the vertices of the triangle are all different, and labelled counterclockwise, the edge numbers will all be 1 and the circled number in the centre of the triangle will be 3.
- If the endpoints are all different, and labelled clockwise, the edge numbers will all be -1 and the circled number in the centre of the triangle will be -3.
- If the vertices of the triangle are all the same, the edge numbers will all be 0 and the circled number in the centre of the triangle will be 0.
- If two vertices are the same and the third is different, one edge will be labelled 0, another 1 and the third -1. So the circled number in the centre of the triangle will be 0.
Look at edge AB of the original triangle. In moving from A to B, a number 1 indicates a change from A to B, the number -1 indicates a change from B to A, and the number 0 indicates no change. Since the overall change is from A to B, the sum of the numbers along AB is 1. Similarly, the sum of the numbers along the edges BC and CA of the original triangle are each 1.
So the numbers along the outside edges of the large triangle add up to 3.
The numbers along the inside edges add up to zero, since an inside edge will either be labelled 0 on both sides, or 1 on one side and -1 on the other.
Thus the sum of all the edge labels is exactly 3.
Now the sum of all the edge labels must be the same as the sum of the circled numbers inside the small triangles. Thus the sum of the circled numbers is 3. Since the circled numbers are either 3 (for a small triangle labelled ABC counterclockwise) or -3 (for a small triangle labelled ABC clockwise), the number of counterclockwise triangles must be exactly one more than the number of clockwise triangles.
And that is exactly what Sperner's Lemma predicted.
You may also like
Fixing It
A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?
OK! Now Prove It
Make a conjecture about the sum of the squares of the odd positive integers. Can you prove it?