 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tower Hamlets Leadership for Learning Project 2016-17
NRICH has been invited to lead a series of linked face-to-face PD days for primary teachers in the London Borough of Tower Hamlets over the academic year 2016-17, focusing on Leadership for Learning in mathematics. Two teachers from each of 25 primary schools will come together on each day with two members of the NRICH primary team to explore ways of integrating the three aims into
the primary mathematics curriculum and to consider how best to support their colleagues in developing appropriate strategies for problem solving, reasoning and fluency in their classrooms.
Each session will offer opportunities to explore the role of NRICH tasks in nurturing confident, resourceful and enthusiastic teachers and learners of mathematics, and gap tasks will encourage the development and embedding of these ideas in their schools throughout the year.
This page summarises the content and discussions during each day. If you would like anything uploading to this page, or have any queries about the project, please contact the NRICH primary team.
Day 1: Thursday 20 October 2016
Here is a pdf of the PowerPoint slides we used on the day: 20161020TowerHamletsDay1.pdf
In session 1, we explored the difference between rich tasks and 'low threshold high ceiling' (LTHC) tasks by having a go at Magic Vs, then Baravelle. We discussed how we need to plan differently for these different types of tasks. Rich tasks may need tweaking so that they are accessible to all children, whereas by definition,
the starting point of a LTHC task is accessible to all but the teacher will need to prepare questions that stimulate deeper mathematical thinking. The pdf linked above gives detail of further support on the NRICH website.
Session 2 focused on drawing attention to the seven key problem-solving skills that NRICH suggests are important for primary children to experience:
- Trial and improvement
- Working systematically
- Pattern spotting
- Working backwards
- Reasoning logically
- Visualising
- Conjecturing
We engaged with the following NRICH tasks to exemplify these skills: Two-digit Targets, 6 Beads, How Would We Count? and Money Bags. Our Problem-solving Feature includes an article which discusses these key skills in more detail along with groups of tasks which lend themselves
to developing each skill.
Just before lunch, we discussed the idea that participants will keep a reflective journal throughout the project. Notebooks were given out for this purpose, although individuals may choose to record their journal in whatever way suits them. The aim of the journal is as a vehicle for delegates to reflect on sessions and time between sessions, for example by jotting down 'noticings',
and as an aide-memoire. They are personal for individuals and so will not be 'looked at' by anyone else.
Time was also given for delegates to jot down what they, as individuals, were hoping to gain support for, or hoping to develop, over the year. Here is a record of everyone's thoughts, which will be followed up next time.
Session 3 focused on the role of the teacher in the context of a problem-solving classroom. We worked on a version of Domino Sets in which groups had to decide whether the set of 0-9 dominoes was complete. Here are some photos showing us engaged in the task:









We then tried a follow-up task, Amy's Dominoes, and discussed how we might have had a different experience of this task if we had not had the opportunity to engage with Domino Sets first.
We mentioned research by Kenneth Ruthven which suggests a model for teaching mathematics: exploration -> codification -> consolidation, rather than a 'show then practice' model found in some mathematics lessons. Although the context is secondary mathematics, this feels very relevant for primary too. You can read the paper, published in Educational Studies in Mathematics 20
(1989) here: ExploratoryTeachingKRuthven.pdf
We spent some time considering the kind of questions and prompts we might want to use to stimulate high order mathematical thinking and reasoning, linked to Bloom's Taxonomy. For further details and a link to the question prompts, see our article which describes Bloom's Taxonomy.
We then had a go at a magic square task from the book 'Mathematical Team Games' by Vivien Lucas:


This led to a discussion about the teacher being a 'guide on the side' rather than a 'sage on the stage'. We also mentioned the idea of 'yoyos', which we heard about from another teacher - placing a yoyo on a table indicates 'you on your own', encouraging that group of learners not to seek assistance from the
teacher.
We talked about desirable teacher behaviours and the following points came up:
- valuing mistakes and learning from them (or 'making meaning' rather than 'making mistakes')
- valuing everyone's contribution
- not being the 'font of all knowledge' but encouraging a community of mathematicians working together
- trying not to let body language/tone of voice imply that a learner's response might be incorrect/correct
- asking 'good' questions which probe thinking
- valuing ways of approaching a task, not just answers
We shared some research by Mary Budd, which revealed that increasing 'wait time' from 0.9 seconds to more than three seconds has a massive impact on the classroom. This is summarised in the above linked pdf of the PowerPoint slides.
Time was left towards the end of the day for colleagues from the same school to talk about how they would each implement some of today's content in their classrooms.
Expectations for next time:
- Put planning into action back at school
- Record relevant thoughts in reflective journal
- Read chapter 2 of Jo Boaler's Mathematical Mindset book (a copy has been given to each school)
Day 2: Thursday 24 November 2016
Here is a pdf of the PowerPoint slides we used on the day: 20161124TowerHamletsDay2.pdf
Sessions 1 and 2 focused on the problem-solving process, which NRICH suggests comprises four stages:
Stage 2 - Working on the problem
Stage 3 - Digging deeper
Stage 4 - Concluding
We looked at each stage in more detail by trying a task together. To illustrate stage 1 (getting started), we had a go at One Big Triangle. As delegates worked on the task, the following comments were overheard:
- Is that the only way of doing it?
- Why don't we ”¦?
- What do the colours mean?
- I wonder what would happen if ”¦?
- Shall we just start again?!
After some time, Fran asked how participants had got started on the problem. These strategies were shared:
- Picking a random number
- Starting at the top
- Building the shape of the large triangle then 'fiddling'
Fran noted that interactivity included in the task helps to narrow down the possible arrangements because the tiles are not rotatable (in contrast to the physical pieces which delegates were using). We had more time working on the task, perhaps 'magpie-ing' an idea for how to proceed which had been offered by others, or perhaps challenging ourselves to find a solution where the colours
meant something and where the colours seemed irrelevant (inspired by one of the overheard comments).
Once we had spent more time working towards a solution (or more than one), we shared further strategies:
- Trying to look at the frequency of numbers and placing those with duplicates on the edge
- Focusing on 9, 5, 1, which we thought might be key
- Rotating our tiles to match the orientations in the interactive
- Starting on 5s - there are three, so one must go on the outside (NB this is a good opportunity to elicit reasoning)
- Wondering whether the colours were going to make a pattern round the edge, for example, or whether they would match
- Trying to keep track of what we had found so far e.g. by taking a photo (this could lead into comparison of two group's solutions)
We discussed how we could tweak the task to make it more accessible and suggested:
- Giving out the pieces and inviting children to make number bonds to 10 in pairs
- Starting with a smaller triangle - trying a simpler case
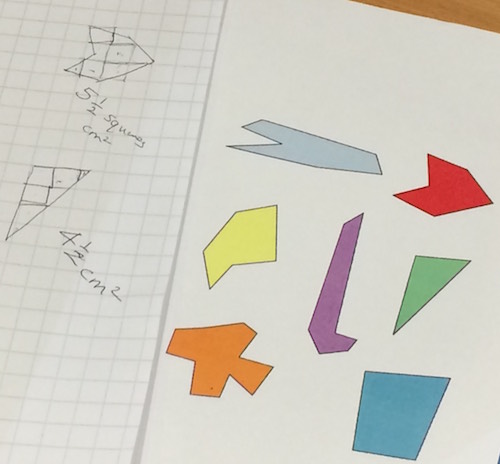
To illustrated stage 2 of the problem-solving process (working on the problem), we had a go at Reflecting Squarely. Fran showed the image of the three pieces and invited us to discuss what questions sprang to mind. The following were shared:
- Can you put them together to maximise the number of lines of symmetry?
- What is symmetry? Ask something like, “Could you choose one shape and show its lines of symmetry?”
- How many different ways can you make a shape with lines of symmetry?
- How many different ways can you fit the shapes together? Which of those have a line of symmetry?
We focused on the third question, so delegates were challenged to find all the different ways that the three shapes could be fitted together (edge to edge with no overlaps) to make shapes with line symmetry. Here are some photos of us working on the task:




As delegates worked, these comments/questions were overheard:
- If you turn it around is it the same shape?
- Have we done that already?
- That piece isn't touching completely.
Fran invited participants to offer any hints to those who might have hit a brick wall:
- Consider different orientations of the line of symmetry
- Think about shapes that have a line of symmetry e.g. letters of the alphabet and see if you can make them
- Take one arrangement and see if you can morph it to make another solution
We looked at the solution which had been submitted to this task on NRICH and our challenge was to look at the system that Andrei uses and to try to replicate it, then to find out which solution he has omitted. There were discussions about what is the same and what is different. One delegate justified their group's approach “we end up with the same
shape, but used the pieces in a different way to get there”, in other words they were looking at positioning of the pieces, not simply the outline of the resulting shape.
Fran commented that she had overheard a few people saying something like, "I'm not very good at shape or seeing things". If we allow children to say this, they are limiting themselves. If they don't believe they can do something then chances are they won't. Fran mentioned a quote which she'd seen on a colleague's classroom wall, which is rather powerful: “Whether you think you
can or whether you think you can't, you're probably right”. Instead, we discussed encouraging statements like “I'm not very good at shape or seeing things YET”, which portrays a different mindset.
Towards the end of session 1, we looked at the key themes that had arisen when participants were asked last time about what they would like to get out of the whole PD programme. Every individual comment is recorded here, and these are the common themes:
Fran noted that problem solving and reasoning were also identified by several delegates but these are a planned focus for future sessions already so haven't been included in the grid above. She also pointed out that END, EYFS, current research and modelling (all of which were identified by multiple delegates) will be all pervasive through the six days. Participants discussed
these themes on tables and then decided which one or two they (as an individual) would particularly like to focus on throughout the year.
In session 2, we moved on to examining stages 3 and 4 of the problem-solving process. To facilitate discussions about stage 3 (digging deeper), we played Got It. We played the game against the computer and when the total reached 18, with our turn next, there were several comments:
- It doesn't matter what we do, we've lost.
- Unless it's a thick computer!
- We need 5, which we can't have. So we can't make 23 and the computer can.
Liz asked how we might play differently next time, which led to a discussion about whether we want to make the computer get to 19. Other suggestions included going for 4 first to start off with. The following exchange took place:
“You've got to think ahead, around the 15 mark, so that we can get to 18.”
“If we do 13, they'll add something and then we can get to 18.”
Liz suggested having another go to see if we could guarantee getting to 18. One participant came up with the numbers 23, 18, 13, 8 and 3 to use as 'stepping stones' which Liz wrote up on the board. Liz invited everyone to think about how we could use this information to help us beat the computer. After some discussion in pairs/small groups, one group was able to use the
numbers listed to beat the computer. Delegates were then encouraged to play against their partners and either consolidate the strategy that had been demonstrated or to explore how they would go about trying to win when the total is changed to 22. Having successfully beaten the computer with that new total, we then changed the range of numbers so that the game allowed players to add on
1, 2, 3, 4 or 5 each turn (still aiming to make a total of 22) . Finally, we stuck with the same range of numbers (1, 2, 3, 4 and 5) but changed the goal to 24. One group said, “We'd like to change the settings. We went back in 6s from 24 and got to 0, so we want the computer to go first.”
Liz invited delegates to try to articulate a general strategy for beating the computer. When will we want to go first and when will we want to go second? One participant offered, “If the target number is a multiple of the bond you're making with the numbers you're adding, you want the computer to go first”. Another clarified, ”If it's not a multiple of the bond
(which is the largest number plus one) you want to start”.
Liz commented on the way participants were posing their own questions as they tried to work out a strategy. This is one of the things we're looking for in the classroom in order to deepen the mathematics and demonstrate the power of the mathematics to stretch children's thinking. In this game, we can use mathematics to generalise the strategy completely, so we can win the game no
matter what the target number and no matter what numbers we are allowed to select from. (Liz suggested always using a range of consecutive numbers, starting with 1, as numbers to pick from, otherwise there is a risk that the game becomes overcomplicated and difficult to analyse.
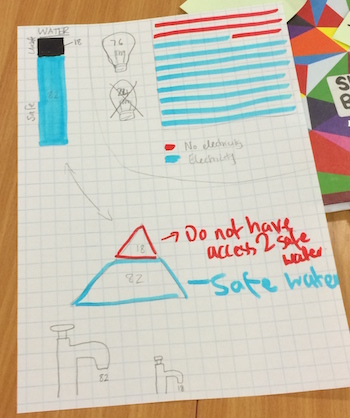
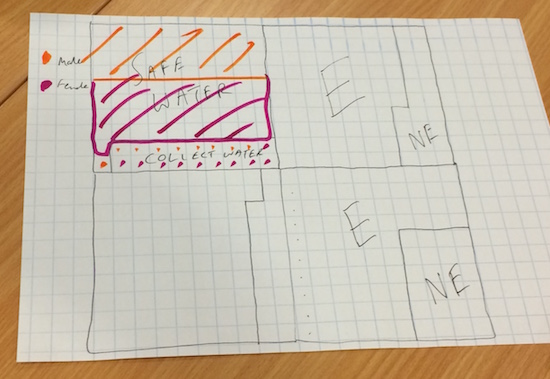
To focus on stage 4 of the problem-solving process (concluding), we had a go at If the World Were a Village. This activity was inspired by the book of the same name, in which the world's population is represented by a village of 100 imaginary residents, meaning that each villager represents about 67 million people. First, delegates were asked to look at the three
different images of 100 people and decide which shows 100 people in the best way. Here are some thoughts:
- One participant found the right hand image 'disturbing'
- One said “the one on the left is tidier”
- Another said, “it depends on what you want it to show”
With the last point in mind, delegates were asked to select one of the two sets of data given on the slide (see pdf link above) and to have a go at representing it in some way. Here is a sample of the results:
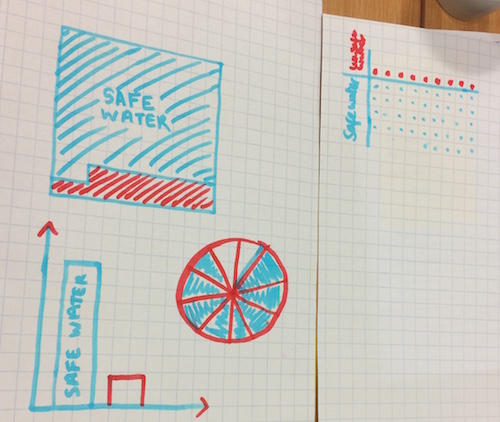
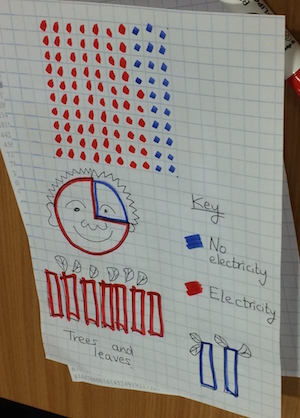
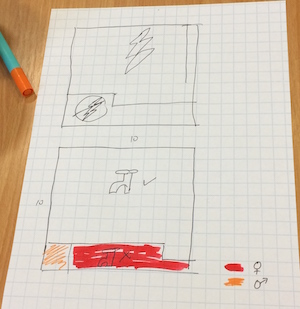


Time was allowed for everyone to view all the resulting representations and a general discussion ensued. Some commented on the creativity of others and how it was more powerful if the representation somehow incorporated imagery which linked to the data.
We discussed what stage 4 of the problem-solving process might look like in the case of this particular task. It might be that you could facilitate a conversation about learners' views on which was the most effective representation and why. It might be that you would share data representations from other sources with a class, so they could pull out the key features. Fran recommended
the book Information is Beautiful by David McCandless, which is a great source of infographics. Liz referred to Kenneth Ruthven's research, which was mentioned last time and is linked above, in the sense that stage 4 potentially offers an opportunity for teachers to 'codify'
learning i.e. drawing out how this task lends itself to the consolidation of what children already know and how this new knowledge fits into their existing understanding.
We then took some time to reflect on the morning's content, through the lens of the chapter we read in Jo Boaler's Mathematical Mindset book. Delegates had been asked to read chapter 2, which focused on making meaning rather than making mistakes. The following comments were made:
- Support of the whole school and parents is crucial
- Starting early with these mindset messages is key
- Resilience is hugely important to build, wrong isn't bad, try to approach it in a different way
- Schools experience a tension between testing and developing the mathematicians they want to (Liz mentioned research that shows a problem-solving approach doesn't hamper test-taking ability, see for example some of Jo Boaler's work on her Youcubed website)
- Changing the vocabulary can support moving the mindset - having up alternative sentence structures to model these for children
- It's not too late for children by Y6, the messages we give them affect their mindsets and can make a difference as soon as expectations are clarified (for example, about maths not having to be fast or just about finding the answer)
Just before lunch, delegates were given the opportunity to talk to colleagues about what they had tried out in their own classrooms since last time. Fran and Liz posed the following questions:
- What went well?
- Were there any surprises?
- What might you do differently next time?
Each table pulled out key points and recorded them on flipchart paper:





We began session 3 with Dice in a Corner. Fran deliberately didn't reveal the focus of this session as she didn't want to influence what delegates said and did. Fran explained that this task had been created for the National Young Mathematicians' Award (see this brief article and this linked
feature for further information) so has a high ceiling. Having had a while to get started on the task, Fran asked participants to share their noticings or any strategies that might be helpful to those who are stuck, which produced the following:
- When you find one solution, try rotating the two end dice
- Using higher numbers as the glue makes the total smaller
- If you hide one high number then the other one hidden will be low because opposite faces add to 7
- Work systematically, for example you could work through the numbers that are hidden in numerical order
These comments/questions were overheard as delegates continued to work on the challenge:
- How about ”¦?
- I think we're going to have to try ”¦
- What if we ”¦?
- Let's prove that ”¦
There was chance for us all to look at everyone's work. Here are some examples:

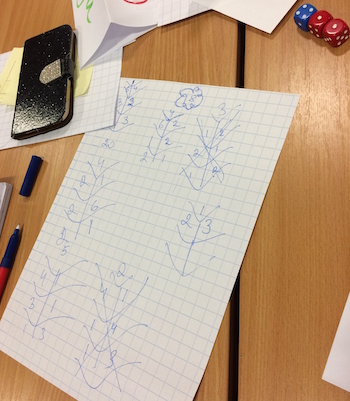

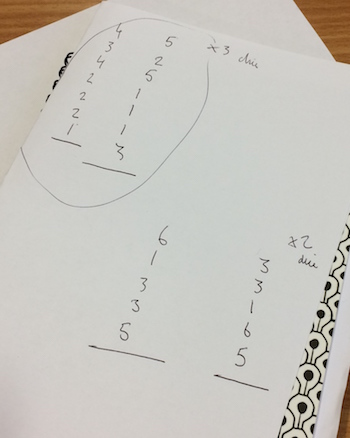

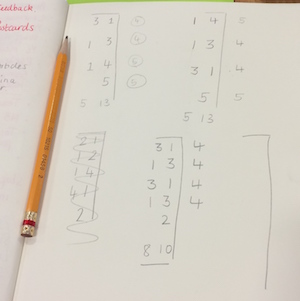
This produced the following comments:
- Ah people recorded! I didn't do that.
- Oh algebra!
We talked about the task more generally and a conjecture was offered - it can't be done with just one dice. Fran asked how we would begin to prove this. One delegate responded: "Only three faces are on show, so even with the largest amount possible (4, 5 and 6) you're not going to get 18". Another group thought that it wasn't possible to have a total of 18 using more
than five dice as for five dice they had all 1s and 2s showing, with one 3, so they thought that if they added in another die, the total would automatically go above 18. Fran commented that limiting this very open problem by encouraging children to reason why they can't use fewer than two dice or more than five dice works well.
Fran reminded of everyone of 'yoyo' moments (you on your own, as mentioned last time). As learners are working on this task, the teacher's role is listening - not talking is very difficult. Fran emphasised that we should try not to make assumptions that thinking isn't happening, even if we can't see anything
happening!
We were then asked to imagine that we were a pair of children (or a group of three) feeding back to the rest of the class about the task everyone has been working on. How would we communicate how we went about the task and what we have found out, bearing in mind that each pair would only have a couple of minutes to give their feedback? This led to a discussion about the possibility of
using the problem-solving process sheet as a prompt. We also talked about how it feels to be told that anyone in the room can be chosen to feedback, rather than the teacher selecting a pair who have their hands up.
Fran then revealed that the focus for the afternoon session is recording. She encouraged delegates to have a look back at any recording they had done as they worked on the tasks today and asked why they had recorded in each case. The following reasons were given:
- To help remember what I have done
- To help with 'pattern sniffing'
- To help me work out where I am going next if something hasn't worked
- To explain it to myself
- To prove a point
- To speed up the process, perhaps using a shortcut method
- To model or visualise to help further thinking
- To avoid repetition
- To help explain it to someone else
- To help me follow a system when I am working systematically
One delegate wondered whether the amount of recording they do is affected by how much they are engaged with, or enjoying, the task, but there seemed to be differing opinions amongst the group as to what exactly the effect might be.
Fran emphasised that recording for a purpose is key. We talked about taking photos as a record of problem solving, no matter what methods have been used so that we value all children's mathematical recording. Fran referred to NCETM's marking policy, which can be found on the NCETM website - note you will need to be logged on to the site in order to access it.
(For NRICH's suggestions about reasons for recording, see the pdf of the PowerPoint slides linked above.)
Liz then introduced Lots of Lollies, which had been chosen as it lends itself to such a variety of recording methods. We explored the task for ourselves, but particularly considered different ways of recording. Having had a look at the way other people recorded too, Liz asked how, as the teacher, we might draw out the variety of recorded work and celebrate
particular features. This prompted the following comments:
- There can be a tension between school policies and the creativity of the children, for example: emphasis on 'one digit per box' in Y1; schools not accepting that rough work fits with their presentation policy; squared paper versus plain paper.
- You could put three different methods under the visualiser and discuss “what do you like about this way of recording?”
- Liz commented that she didn't think she would ever be in a position to say which is the best way of recording a task. She could justify the method she chose, but she wouldn't want to draw out a 'best' way as it would be unlikely to be 'best' for everyone.
- It's important to give children a chance to try out different ways of recording to see what suits them.
- Ask children why that particular way was better for them to encourage discussion about effiiciency for that person.
- We could ask “What might the disadvantages be of each of these?”
- One participant said he has the seven key problem-solving skills up on the classroom wall and they talk about how each method of recording might support a particular problem-solving skill.
Liz drew attention to the NRICH Recording Mathematics Feature that includes an article and tasks which particularly lend themselves to discussions about different ways of recording.
One delegate jotted down a question on a post-it towards the end of the day: How can we get young children to record without just showing them how to do it?. This article, written by Elizabeth Carruthers and Maulfry Worthington, is well worth a read. The authors use the term 'children's mathematical graphics' to refer to the visual marks and
representations (graphics) young children choose to use to explore mathematical meanings and communicate their thinking. They distinguish between 'recording mathematics' and 'representing mathematical thinking', whereas in our session we have bundled these all together under the term 'recording'. They conclude that focusing on mathematical mark making with young children and providing
an environment that encourages learners to choose their own mathematical graphics are key.
In a similar way to day 1, time was left towards the end of the day for colleagues from the same school to talk about how they would each implement some of today's content in their classrooms. We also discussed briefly the possiblity of beginning to think about how to disseminate ideas from our days together with colleagues back at school (this might take the form of encouraging a colleague
to have a go at an NRICH task with their class, or it could mean leading a whole staff meeting, for example).
Expectations for next time:
- Put planning into action back at school
- Record relevant thoughts in reflective journal
- Read chapter 5 of Jo Boaler's Mathematical Mindset book (a copy has been given to each school)
- Begin to consider dissemination to colleagues at school
Day 3: Thursday 19 January 2017
Here is a pdf of the PowerPoint slides we used on the day: 20170119TowerHamletsDay3.pdf
Sessions 1 and 2 focused on exploring progression in reasoning. We started session 1 with Dicey Addition and Fran invited participants to discuss what they could articulate about their reasoning once they had more than one go at the game. Comments included:
- We began to plan ahead. For example, we asked ourselves, would it have been better to have got a 1 later in the game?
- The first time we played it was random, then we started looking for number bonds. There is joy in playing randomly to start with (Fran pointed out that this links to Ruthven's research mentioned on day 1 'exploration, codification, consolidation').
Fran moved everyone on to the addition version of Dicey Operations. The following comments were overheard as delegates played:
- Ooh hoo - I beat you!
- Oh no ”¦ (before a number was placed - Fran pointed out that she would want to ask a learner why s/he had said that)
- Argh ”¦
- [Intake of breath!]
There was also a sense of keeping your decisions secret from your opponent's.
Fran invited participants to consider how they would structure these two games in order to help children develop their reasoning. Here are the responses:
- It is valuable to just play a number of games first - it's important to give time to explore before asking learners to think about their thinking.
- Giving time to get going then having some feedback about what they have found so far would be helpful (Fran suggested asking for 'noticings' which can't be wrong. One way to phrase this in the classroom is to say “I'm interested in knowing anything you know”.)
- You could have a number of grids on the board and ask them to explain a winning strategy, or why one way was more successful than another; you could pre-prepare a completed grid that hadn't gone well - perhaps pupils could guess which order the numbers were placed.
- At a particular moment, ask which number that child would like to throw and why - they could write down their response or talk to a partner.
- Noting down vocab that you hear on the board would mean that others might be more likely to use it for themselves.
- A player could deliberately choose to try out a particular strategy for winning the game.
- Play in teams rather than as individuals to stimulate discussion e.g. pair against another pair.
Fran suggested delegates have a go at playing in teams and she asked what was different when playing team vs team compared with playing 'one on one'. Here are participants' comments:
- You articulate strategy and reasoning.
- An example of the discussion in one game centred on a 'controversial zero'! The winning team placed a zero in the hundreds column but the other team felt that didn't result in a three-digit number and, as the game involved adding three three-digit numbers, it should not be allowed. However, looking again at the instructions for the game, there is no mention of three-digit numbers so perhaps allowing a zero in the hundreds column is ok. (This is in contrast to the task Two-digit Targets which we explored on day 1.) It was pointed out that it might be the case that a team has to place a zero in the hundreds column if zero is the last digit to be rolled and there is only a hundreds space free.
Fran summarised that playing team on team results in a richer experience but having the chance to explore individually first feels like a more natural progression.
Liz outlined NRICH's suggested progression in reasoning, which has five stages:
- Describing
- Explaining
- Convincing
- Justifying
- Proving
and she summarised what was meant by each one (see the article Reasoning: the Journey from Novice to Expert for more detail). It is important to note that this progression is not age-related; in other words proof is not just for upper KS2 children. One delegate asked about the nature of 'justifying' and Liz explained that it would usually refer more to the
structure of the mathematics than 'convincing' might.
To delve into proof, we tweaked Dicey Operations so that this time the dice was thrown nine times before placing any of the digits. The challenge was to decide how the digits should be placed so that the total was as close as possible to 1000. Delegates were asked to develop their reasoning so that they could convince another pair that their arrangement
was the best, and ultimately, to prove that their way resulted in the closest possible answer.
Having worked on the task for a while, we shared some solutions and the following contributions were made:
- You'd have to have worked out all of the possible solutions with all nine digits in order to prove an answer.
- You wouldn't need to use the lower numbers in the hundreds position, because you couldn't make the number big enough.
We concluded that, for this task, using logical reasoning means we do not have to find all possible ways of arranging the nine digits in order to create a proof.
This led into a discussion about what we take for granted mathematically. What are the accepted 'knowns' in mathematics? Does your own experience dictate what you use in order to prove something? Liz suggested that the more examples children experience and the more modelling they see, the better able they are to reason in different situations.
We moved on to having a go at Three Neighbours, which Fran and Liz had deliberately selected because it offers great opportunities for proof. Some of the initial noticings included:
- If the first number is odd, there'll be two odds.
- The sum is odd if the first number is even.
One group used a systematic approach, trying numbers 1, 2, 3 then 2, 3, 4 then 3, 4, 5 and so on. They found that the sum was always a multiple of three. They weren't sure why, but tried some larger numbers and noticed that the digital roots were always 3, 6 or 9.
Another delegate thought that getting a multiple of 3 didn't work if you used negative numbers, for example -1, 0, 1. However, this led to a discussion about zero being a multiple of every number so in fact this example does work. That group asked their own questions about larger groups of numbers and whether they would behave in the same way.
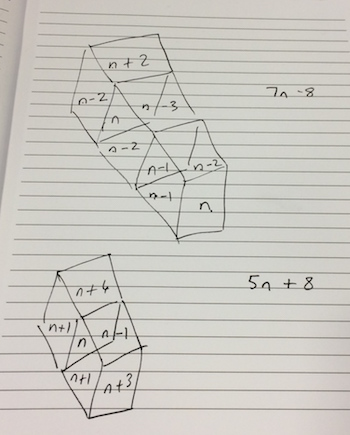
Liz asked how we might prove that the sum of three consecutive numbers is always a multiple of three. One participant shared a visual array proof. Another added that it worked similarly for five numbers (the one less 'balances' with the one more and the two less balances with the two more). Another delegate conjectured that it would work for any odd number of
consecutive numbers.
An algebraic proof was also shared, whereby the three consecutive numbers were labelled (n-1), n, (n+1) and this was discussed.
Liz drew attention to three different ways of communicating proof:
- Visually
- Algebraically
- Through a series of statements (written or spoken)
She also outlined what NRICH sees as five methods for proving, accessible to primary children:
- Proof by counter-example - an example that doesn't work disproves the conjucture.
- Proof by exhaustion - this depends on there being a small number of results so that it is manageable to find all possibilities; it is about working systematically.
- Proof by contradiction - we assume that what we want to prove is not true, and then show that the consequences of this are not possible.
- Proof by logical reasoning - the chain of reasoning is complete, with no room for ambiguity and no missing steps.
- Generic proof - a carefully selected example enables anyone to see, in that example, the general structure.
(For more detail on the above, see our article Mastering Mathematics: the Challenge of Generalising and Proof.) Liz explained that we will look at examples of these different methods during subsequent days together too.
In session 2, we began by sharing classroom experiences since we last met. Fran invited us to do this through the lens of the chapter on rich tasks we had read from Jo Boaler's Mathematical Mindsets book. Tables wrote up key points on flipchart paper, which are included below, and there were a few general comments:
- Children were very engaged, not wanting to stop
- Some questioned whether this is Maths! Isn't there just one answer?
- Benefits of collaborative working were observed - supporting those who were struggling, challenge of explaining clearly









Fran introduced another task, Strike It Out, and we watched the simulated game. Fran asked us to consider:
- How do you think you play?
- How do you win?
- Do you have any questions?
During the competitive version of the game, Fran shared the fact that she had overheard conjecturing and that she had noticed different ways of recording. Fran led us on to a collaborative version of the game and we explored whether it is possible to create a string of number sentences that uses all the numbers on the 0-20 number line; the 1-20 number line and any number line with a set
of consecutive whole numbers. Here is a selection of comments for each scenario:
0-20 number line - not possible
- Can't use the zero as you would have to use the same number twice e.g. 20-0=20, repeat 20 or 19+0=19, still repeating 19
- It is alright to have emergent thinking - we don't want to give the impression that to offer an answer, it must be completely polished
- We might tweak the task to be more child-friendly, for example by cutting up a string of number sentences and muddling them up and challenging learners to put them in the right order
1-20 number line - not possible
We managed a string of number sentences, but without using the number 10. Think it's because you've got twenty numbers. We start by using three numbers; then in the next turn we use two more numbers; then in the third turn we use another two more numbers etc. We are never going to use twenty numbers, instead we will get to twenty-one or nineteen numbers. We might be able
to do it with numbers 1-21. However, because it is feasible it doesn't necessarily mean it's possible.
Fran commented that it is encouraging to hear conversations such as "is that the sort of thing that constitutes proof?” Fran asked delegates to consider the five stages of reasoning in the context of Strike It Out. What did they say that might fit with each stage? What might children say that would indicate they were working at a particular stage? Here
are some contributions to the subsequent discussion:
- Children might struggle to question the structure of the game rather than the numbers themselves. Fran shared the analogy of everyone in the class being on board a ship and the teacher encouraging those who are exploring more thoroughly to be like a deep sea diver (bringing things back to ship to share with everyone) rather than a jet skier (racing off into the distance, leaving everyone else behind). Fran suggested that it might be possible to query the number of numbers left if no-one comes up with this themselves; however she pointed out that we should remember that we don't have to get the children to this 'finishing point' - it is about moving along the continuum and making progress along the reasoning journey.
- Working mathematically means that you might encounter dead-ends.
- Sometimes you can see a pattern which actually has arisen by chance e.g. all the games one group played happened to use fifteen numbers.
- The prevelance of computer games means that children are prepared to try things out and not be bound by rules. If we work on 'traditional' mathematics tasks, putting pupils in a situation when there is just one right answer, maybe we shouldn't be surprised if this results in failure. Perhaps learners do not expect to bring experience from other settings to mathematics ...
In session 3, Liz gave a brief overview of Jo Boaler's research, in response to questions last time about evidence to support a problem-solving approach. Full references are included on the final slide of the PowerPoint pdf, linked above, and many links can be found on Jo Boaler's website in the research
articles section or the short impact papers section. (NB The most recent article in the latter section is directly relevant to these discussions but was in fact published on the website after this day.)
We then spent some time exploring the Celebrating Solutions Feature, which focuses on how children's solutions to NRICH tasks can themselves be used as a teaching resource. We began by looking at how published NRICH solutions could be used with children as a way of anaylsing others' reasoning. We did this by having a go at two different tasks in table groups
- Sizing Them Up and Forgot the Numbers. These were both structured in the same way so that we had some time to consider how we would solve the task ourselves, but then we were invited to look at some children's starting points and, in pairs, develop a particular starting point into a full solution (see the teachers' resources section of each task for
full details).
Here are some photos of delegates working on these tasks:



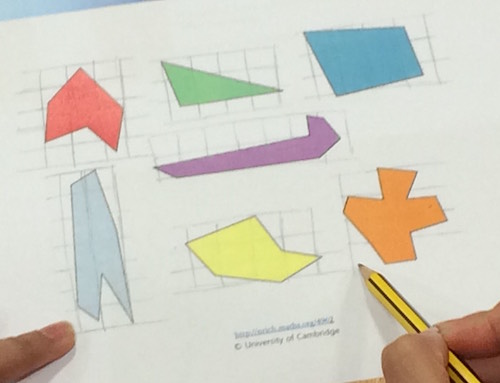

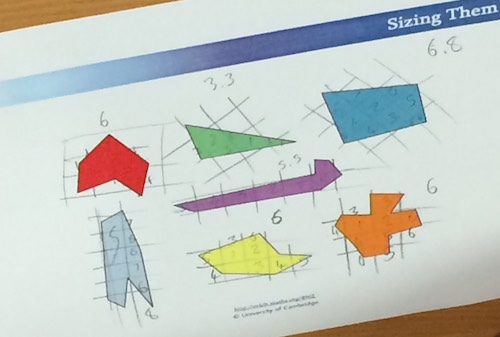

We talked about what 'getting inside' someone else's answers can do for us and here are some responses:
- One of the skills of the teacher is doing this when marking children's work
- It made us re-evaluate the question (for example in Sizing Them Up, we hadn't thought of using length as 'size')
- It helps us 'see' what good reasoning looks like
- One delegate mentioned Shirley Clarke (who has written books and runs courses on 'Transforming learning through formative assessment'), and suggested that you could offer a choice to groups - either they could start the task themselves or choose to start with someone else's method.
We then used published solutions on NRICH in a slightly different way. We had a go at solving the Heads and Feet task, and then looked at the published solutions from a teacher's point of view, asking ourselves:
- What does each solution show that the learner knows?
- What understandings have been demonstrated?
- What might each child need to work on?
In this way, we simulated a way in which NRICH solutions could be used in a staff meeting, for example, to provoke conversations around assessment.
Liz summarised strategies which may help learners communicate their reasoning (see the pdf of the PowerPoint presentation above) and explained how we had focused mainly on 'understanding how others work' today, but that we will explore the others in more detail next time.
In the penultimate session, Fran introduced us to KenKen puzzles and we watched a clip of some girls explainig how they were going about solving a KenKen. We picked out examples of novice, proficient and expert reasoning:
- Example of one girl who is at least proficient as she was able to explain the 'dog-leg' idea
- The girl who was more novice said, "I start with the adding as that's the easiest" - she had not grasped the idea that the 'hook' in doesn't necessarily come from the ease of calculation
- The second girl offered possible solutions as opposed to proving why they work, which the first girl did better.
Fran invited us to consider where the children we teach would rank themselves in terms of the progression in reasoning.
Fran quoted Gattegno as saying "If it's not shot through with infinity, it's not mathematics" in encouraging us to focus on generalising and proof in our classrooms.
Once again, time was left towards the end of the day for colleagues from the same school to talk about how they would each implement some of today's content in their classrooms. Fran and Liz encouraged participants to jot down questions for them on post-its, of which there were a few. A couple were addressed there and then, but two will be incorporated into day 4.
Expectations for next time:
- Put planning into action back at school - try one of the live tasks from the Celebrating Solutions Feature
- Record relevant thoughts in reflective journal
- Read chapter 9 of Jo Boaler's Mathematical Mindset book (a copy has been given to each school)
- Try out an activity with colleagues and analyse children's solutions together (either those published on NRICH or your own children's work)
Day 4: Thursday 02 March 2017
Here is a pdf of the PowerPoint slides we used on the day: 20170302TowerHamletsDay4.pdf
Sessions 1 and 2 focused on exploring progression in reasoning, building on the content of Day 3 in January.
Session 1 started with some reflection about where teachers felt their class, and in some cases their school, was on the reasoning journey. A prompt list of the tasks explored on Day 3 was provided, whilst groups discussed how the implementation within their settings was progressing. Tables wrote up key points on flipchart paper, which are included below, and a
book called Concept Cartoons by John Dabell was recommended as a useful prompt for classroom discussion. A Tower Hamlet's document called Progression in language structures was shared by Andrew from Cubitt Town Junior School. This covers a variety of language, but there
is a particular section on mathematical explanations which delegates may find helpful to refer to.









Next participants worked on Make 37 and Liz invited them to discuss ways in which they could convince themselves and others about their mathematical reasoning. Comments included:
• “If you have an even amount of odd numbers you get an even answer. If you have an odd amount of odd numbers you get an odd answer.”
• o+o= e
o+o= e
o+o= e
o+o= e
o+o= e
so then taking the answers e+e+e+e+e=e
• A picture of a piece of numicon, and another piece of inverted numicon placed on top of the first, showing that the two 'sticking out pegs' would fit together to create a solid array which models an even number.
One delegate commented that “the brick wall is the clue!” and went on to explain that repeatedly not being able to Make 37, had been the clue he needed to dig deeper and examine the structure of the problem. Not 'letting on' too early with a class (in this case, that the task is an impossible one) was also discussed, because the struggle/effort in attempting to solve the
problem is essential to developing learners' reasoning and determination.
Liz exemplified a 'Proof by Contradiction' for Make 37, and shared the first four paragraphs of an article called An Introduction to Proof by Contradiction, which although it is labeled for Key Stages 4 & 5, contains a clear example which is perfectly accessible in the primary classroom.
In session 2 the 5 types of proof which had been talked about on Day 3 were re-visited along with some methods of communicating these proofs. Fran introduced a Carroll diagram to help act as a framework for teachers' thinking and invited participants to populate the sections with some of the tasks they had encountered on the reasoning days so far, and then to continue
annotating it to support their thinking.
Comments were made about using Three Neighbours (with the image of multi-link towers) and Make 37, as examples of Generic Proof.
The next task was Always, Sometimes, Never (KS1, KS1&2, KS2) taking each card in turn and deciding if it is always, sometimes or never true. Participants were encouraged to justify their reasoning to each other and if they thought the statement was
sometimes true they were asked to come up with cases for each and to try and generalise this. Liz invited pairs to challenge or support each other's ideas when responding, and clarified that 'challenge' in this context didn't necessarily mean disagreement, but could be asking for clarification.
Some discussion points which emerged from this activity are listed below:
In response to the statement "Four-sided shapes are called squares."
• 'Sometimes' - You might have a four-sided shape which is a square; you might have a four-sided shape which is a rectangle; older children might mention quadrilaterals.
• Some younger children might say “yes that's true” so perhaps their first thought might be 'always', but if they know a rectangle, might shift to 'sometimes'. This comment was in reference to the White Rose task about being asked to draw a four-sided shape and thinking that it has to be a square.
In response to the statement "Multiples of 5 end in a 5."
• Expect children to respond 'sometimes' as they might know 10 is a multiple of 5, but it ends in a zero.
More general points:
• Finding a counter example means that you can prove the statement is not 'always' but further reasoning is needed to say that it is 'sometimes' e.g. some four-sided shapes are called squares.
• “When cards were to do with shape, we proved using diagrams rather than logical reasoning.”
• 'Sometimes' statements lend themselves to proof by counter example. “Which might therefore make it an accessible type of proof to explore first with children.”
• “It provides children with the opportunity to have conversations about generalisations, they can then label the method afterwards.”
Pairs on each table used different sets of cards and then rotated to a different pre-sorted set to continue their discussions, seeing whether they agreed or wanted to make any alterations. There was an opportunity for participants to annotate their Carroll Diagrams further, to consolidate and reflect on their understanding and ask any questions that they had.
The last task of session 2 was Jig Shapes. Each member of the group in turn had to describe their card for the others to draw. Fran explained that the describer would have a short amount of time to do this and then each other member of the group could ask a question for clarification. The card would then be revealed,
any points made that could be helpful, and then the next person would take their turn.
Whilst the groups were working Fran and Liz noted down mathematical vocabulary that they overheard, this was shared with participants part way through, so as to support and/or challenge its inclusion in forthcoming 'turns' or prompt groups to make sure everyone understood the collective list.
When asked whether groups felt that they had improved as everyone took their turn, most responded positively. Comments were made about 'magpie-ing' ideas from others, and becoming more specific in their language and descriptions based on previous people's turns.
Other observations made were:
• Very good for talking about properties of shapes, as it can highlight key properties.
• Using different units and fractions which allowed us to be more specific e.g. measurement in mm or "half the way down the left hand side of the square"
• We drew on general knowledge too e.g. "the shape of a house", "like the sun setting" etc.
Groups were then asked to hide two unseen cards from their set, and use the remaining ones to put together the picture like a jigsaw. The challenge then became to draw what the missing pieces could look like, with a focus on reasoning to support what was, or wasn't possible and why.
Participants were given the opportunity to look at the configurations on other tables and judge which locations of the missing pieces were more challenging:
“Two pieces missing next to each other, made it harder to see what shapes were on there. But if the two are in the middle, you have information around the edge which you can draw on.”
“We had two pieces missing which were the only two pieces that one particular shape appeared on, so didn't know that the shape existed.”
“There must be at least one part of the shape visible for you to make conjectures about it.”
“If we had parts of a shape on three different cards, there was less ambiguity about the shape.”
“The orange shape that is not the circle, is tricky to pin down because part of it is hidden behind another shape, therefore we have to make assumptions.”
There were a number of conversations that involved questions about whether particular shapes were regular or irregular. From the discussion on tables, this task was certainly felt to be rich in the variety of opportunities it afforded for the development of language and reasoning.
Following this some time was given to reflect on the different strategies that can support reasoning and Liz explained that we would be exploring each in more depth during the afternoon.
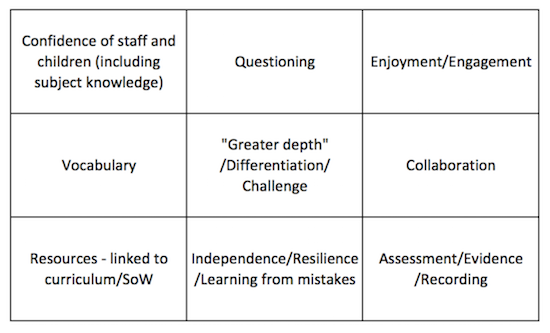
At the beginning of session 3, participants were asked to group themselves according to their chosen focus at the outset of the 6 day programme. Everyone's initial responses had been grouped into the following nine categories:
• Confidence of staff and children (including subject knowledge)
• Questioning
• Enjoyment/Engagement
• Vocabulary
• “Greater depth”/Differentiation/Challenge
• Collaboration
• Resources - linked to curriculum/SoW
• Independence/Resilience/Learning from mistakes
• Assessment/Evidence/Recording
Groups talked about their successes, challenges and progress within each category. Fran explained that there would be a further chance to share experiences on Day 6, particularly to account for those participants whose focus had changed since the beginning of the programme.
In these new groups, the ways in which ideas were being shared with colleagues were discussed. In particular:
• Whether the feature “Celebrating Solutions” (from Day 3) had been used? And if so, how?
• What went well?
• Were there any surprises?
• What might be done differently next time?
The feedback below came from the whole group discussion once groups had each had time to consider and converse:
• Not to simply tell staff, but to model it for them in classrooms with children.
• To do the activities in staff meetings.
• Holding TA meetings to talk about the problem solving skills and now the reasoning. Discussion about the different ways that they could support the children they work with.
• Letting the joy do the conversion for them!
• Copying NRICH's modeling with their own staff.
• Linked to a theme “Curious Mathematicians” for Maths Week. Shared navigating the website with staff and gave them a selection of tasks to focus on 'getting started' to begin with. A helpful 'easing them in'.
• Recognition that there is work to do with parents and encouraging a collaborative approach to working mathematically together.
Within Chapter 9 of Mathematical Mindsets there is a link to a video clip of an American teacher called Deborah Ball with her third grade class. Liz and Fran showed the first 7 minutes of this footage, where the teacher encourages her students to be inquirers and to make conjectures about mathematics.
In the discussion that followed, several key elements were mentioned:
• The time given to allow exploration and consolidation of the children's ideas.
• The minimal, but skilled, input from the teacher. To question, seek clarification and re-focus.
• The autonomous agency given to the members of the class, who appear well used to explaining their ideas and being given the opportunity to do so in discussion with each other.
This footage was used to illustrate the usefulness of opportunities to understand how others work, as a strategy for children developing the communication of their reasoning.
To build on these strategies further Liz and Fran modelled the playing of Reasoned Rounding next and asked delegates to consider:
• How do you think you play?
• How do you win?
• Do you have any questions?
Responses were discussed which included misconceptions about the positioning of the number in the circle depending on whether it had been rounded up or down to reach the nearest ten and then time was given to playing and exploring how the game works and what the opportunities are for reasoning. The different versions offered in the Teachers'
Resources were talked about, as well as the suggestion to encourage pairs to play against pairs in order to support reasoning with a partner.
Liz introduced the penultimate task of the day, Coded Hundred Square and delegates were asked to think about what they were doing at each of the four stages of problem solving (from Days 1 and 2) as they built up their jigsaw solution. Participants were challenged as to “how you would know that you've completed it correctly?” and supplied with
some sentence starters that could be used to provide a supportive framework for learners.
Once again, time was given for colleagues from the same school to talk about how they would each implement some of today's content in their classrooms. Particularly considering their most recent reading from Mathematical Mindsets about Teaching Mathematics for a Growth Mindset, and how other staff could be supported to do this.
The last task of the afternoon was School Fair Necklaces where groups were given bags of counters containing two colours and asked to use them to represent a systematic way of working through their solutions. There was a great deal of discussion about how to go about this, particularly after getting up and going to look at other tables'
systems. Some of the comments are recorded below:
• “I liked the partnering of solutions - had one solution and then its inverse (in terms of colour.)”
• A few people noticed that working with four counters 'unboggled' the mind!
• Some participants said the pattern was more noticeable when fewer counters were used.
• “Looking at someone else's way of working might make you realise that you might have missed something.”
• “Four (counters) didn't unboggle my mind as I didn't think we were considering the whole problem.”
In our concluding comments we drew attention to the feature called Mastering Mathematics:Genralising and Proof and the article within it, gave a reminder about the Primary Curriculum Mapping Documents, and suggested the 'For
Two' tasks as being good for parents and children to work on together.
Day 5: Thursday 27 April 2017
Here is a pdf of the PowerPoint slides we used on the day: 20170427TowerHamletsDay5.pdf
The first slide asked tables to share the responses they'd had from other people about the NRICH/TowerHamlets page on the website (in black pen) and to also record how they had been using the page (in red). The pictures below capture each table's discussions.
Ems introduced session one on fluency. "We're not just looking for solutions, we want students to explain their reasoning."
This has been the focus of her doctoral research; 16 calculations for Y6s were devised and given to children in 20 schools (ranging from Suffolk and Norfolk to the Welsh border). Interviews were arranged to follow up the children's work, and find out what their thinking had been.
Slide 6 shows a learner's attempt at long division. Ems suggested that from a problem solving point of view, long divison could be said to have been mastered when the learner understands when not to do it!
Delegates were shown the calculation on slide 8 and asked to write ideas on post-it notes about what they thought was necessary in order for learners to be fluent in calculation. Feedback from tables was as follows:
- A sense of number. They have it in some cases, but they don't use it!
- Reasonableness - whether an answer is sensible.
- is there any research on the role of tutors? (More tutors in London than elsewhere seemingly.)
- Tutors/parents seem to be introducing strategies earlier than the children meet them in the classroom.
- The boys are more adventurous, the girls less so. There seems to be a large gender difference from SATs: the girls responded positively to being asked to demonstrate algorithms, but struggled when asked to 'problem solve'. Schools are therefore being encouraged to treat calculation as problem solving, rather than teaching it discretely.
- Is it not understanding the concept of subtraction, or not 'seeing' the operation sign?
The different aspects of fluency:
Accuracy
Efficiency
Flexibility
Understanding
Reasonableness
were shared and groups given time to discuss their interpretation of each. Ems referred back to the National Strategy suggestions of:
- Head
- Jotting
- Written
- Calculator
as being a sensible way of proceeding and something which it has been a shame to see less of in classrooms. Delegates were asked how most of their learners would calculate the answer to 702 - 695 and why?
How and why children checked their answers in the research was interesting. Boys generally checked at the end of their work/assessment. Mathematicians report that this is a less productive way of working, particularly in research fields where projects can span years! Do we model this in our teaching? It's not enough to say "don't forget to check". Girls tended to
check their workafter every question. One learner didn't check their answers and when questioned about this, said they had estimated first.
Checking methods in the research included:
- Mentally doing the calculations
- Rubbing an answer out and then repeating the calculation to see if they got the same answer!
- Chosing another strategy to corroborate the answer
- Boys used the inverse, but none of the girls did.
Division and multiplication questions were shared including the task Multiplication Madness for particpants to compare what was the same and what different about different methods.
In the afternoon Fran began session 2 by introducing the activity Little Man. This allowed for some creative curiosity from participants and a very pronounced emphasis on the Reasonableness aspect of fluency, in most solutions.
Brush Loads was the next measures task, and there was much enthusiastic modelling using multi-link cubes! Several mini-plenaries allowed discussion of discoveries to be shared, which impacted on solutions then developed on other tables. Take a good look at some of the pictures below to see if yoy can make sense of the different thinking
that emerged:
Moving on from Measurement to Geometry, Fran introduced the activity Shape Draw. There was a lot of discussion about shape properties, which then moved on to conjectures and generalising.
When participants were asked to reflect throught the lens of the five aspects of fluency, feedback included:
- Accuracy wasn't necessary until there was a need for precise measuremnts, it was more about the need for understanding of the concept
- Some criteria required the reader to define the criteria
- Supportive visual images might help
- Adaptability was needed to redefine your views
- The order of the statements meant that at times the options were narrowed more quickly
- More challenge could be offered by asking whether some cards where more significant than others and if so, why?
Fran discussed the need to allow cognitive conflict and encourage learners to talk about their differing ideas, rather than expecting someone else to 'sort things out' for them. The publications We Can Work It Out (Books 1 & 2) from the ATM were mentioned as
excellent resources which include information that isn't relevent (to be sorted out as part of the problem solving).
Nine-pin Triangles poses the problem "How many different triangles can you make on a circular pegboard that has nine pegs?" Some of the pictures below illustrate the ways in which this problem is often begun.
Discussion initially centred around whether triangles were 'different' if simply rotated? Once it had been decided that they weren't, some participants seemed re-invigorated, as though a more limited number of solutions were within their grasp! Numbers of different types of triangle were shared and then debated. Where there 3 isosceles, 1 equilateral and 3 scalene? Where there
only 7 different triangles in total?
Some systems for identifying the different solutions involved counting the spaces or dots between corners of the triangles. So one recording offered up for discussion was:
5, 1, 0
2, 2, 2
2, 3, 1
0, 3, 3
4, 1, 1
Which prompted some enthusisatic responses from those who hadn't considered this, but now saw a potential way to check their numbers of different types of triangle and a systematic way of checking whether they had found all the possible answers, without needing to draw them all first.
Participants were moved into groups of 4 to try the collaborative task Stringy Quads.
Feedback from how it felt to work together included:
- It required careful use and developmetn of language
- There was a lot of negotiating needed
- We wondered about using the idea from the Nine-pin triangles of each child being a dot
- Visualising was strenghtened from many orientations
- We liked the manipulation of shapes that was possible
- We learnt from discovereis and then redefined the activity/task
- Thoughts about collaborative work/mixed abilities/talk partners (the Shirley Clarke model)
Participants regrouped on their tables for a planning intermission prompted by the following:
- Talking abotu the You Cubed paper "Fluency without fear" (inlcuding the task How Close to 100?)
- How they might intorudce some Homework relfection questions (P.48 of Chapter 4 in Mathematical Mindsets)
- How they would plan for concept compression
- Planning for the embedding of games (either in the form of apps/electronic/other versions) to develop mathematical fluency
The last two tasks colleagues were invited to explore through the lens of fluency in geometry were Poly Plug Rectangles (KS1) and Cops and Robbers (KS1/2 in levels 1-3 of the game).
Comments about playing Poly Plug rectangles centred around the fact that reducing the size of the rectanges (including squares!) increased the difficulty of finding them. Colleagues had some interesting discussions about how they communicated their thinking, what they would expect from learners and how this might be best supported.
Reflection on the Cops and Robbers co-ordinates game was that all five aspects of fluency were required/exercised in the playing of it and that development of learning was aided by discussion ( so to consider playing pair-on-pair, rather than one-on-one).
Day 6: Thursday 8 June 2017
Here is a pdf of the PowerPoint slides we used on the day 20170608 Tower Hamlets Day 6.pdf
Session one began as a continuation of the Fluency in Number focus from Day 5.
Everyone watched the video for Totality with the sound muted. Participants were asked to consider what the rules of the game might be and how it was played. Discussion on tables resulted in some of the following proposals:
• The number you start on links to the total number of moves e.g. Start on 6 mean a link with 6 moves?
• Someone choses a total and you have to reach that total?
• Does the total come from the board? Do players choose two digits to give the starting target?
• Are the colours important?
When Fran prompted with “How are the moves made?” responses included:
• You take turns
• You slide not jump
• You add
The importance of discussion in this exposition was considered. It is key not to assume that children will realise something that hasn't been explicitly stated. Leaners could be asked to share/record their rules and then the rules on the site be revealed to them, for comparison.
Fran clicked the reveal button on the website to share the actual instructions and participants discussed that challenging writing instructions can be tricky and how helpful diagrams can be. Time was given to play the game several times (like learning to drive a car - we need repeated experience, each time will offer something new, in order to consider strategies for improvement) and then
discuss their thoughts.
Discussion began with observations including:
• It's deceptively simple!
• I was thinking about Y2 - it is good for them but in a few goes they can start thinking a few steps ahead.
Fran clarified that this was a low threshold high ceiling task and that as such it might look straightforward, but after a short while there can come realisations that there is more to it and the mathematical thinking can be deepened through questioning.
• We were thinking about how adaptable it is and how you can change the rules e.g. change the operation to multiplication, change to working collaboratively, can we do it in 8 moves/6 moves? What might be the minimum number of moves?
The Teachers' Resources were highlighted - including blank boards to print and fill in with different numbers, linked tasks such as Play to 37 etc. Items to count were mentioned as one way to support playing the game. Totality is an extremely useful game for developing fluency in number, as it can be re-visited by a class throughout the
year.
When prompted as to whether anyone had found any winning strategies, a discussion followed about working across the boards alternating even and odd numbers and how would using zero therefore fit? Participants talked about the opportunities present for deepening reasoning in this way. Responses connected to the five aspects of fluency were that this game reflects the importance of
flexibility and responding to a partner's move, but that it is also important for accuracy to check your answer. The understanding aspect is key to interpreting the rules - learners need time to explore the rules in order to begin to think ahead and play strategically.
We moved on to having a go at Five Steps to 50, where a two-digit number was chosen and then five steps (of either 1, 10 or 100) were taken forwards or backwards to try and reach 50 exactly. Participants were encouraged to collect data as they played - which numbers let you reach 50 in five steps and which don't?
Fran paused 'play' several times to ask for ideas/thoughts/experiences to be shared, and recorded those numbers reported as working or not working in two columns to prompt further testing by others. Time was given for exploration and for discussions to develop about the possibility of generalising which numbers did and didn't work. There was time for talk on tables about which aspects
of fluency had been 'flexed' and Fran mentioned that she'd seen someone tallying the aspects of fluency that they noticed each time; this might be interesting for learners to note too, as a point of development to try and 'see' the potential for each aspect of fluency when they have engaged with a task.
Next the task Shape Times Shape was introduced. As several delegates were familiar with this activity, Fran asked these colleagues to record what they remembered from using it in their classrooms (“What went well? If a learner found a solution quickly, what sort of follow up questions did you ask?”)
Some teachers suggested cutting up the statements and asking learners to order them to support an explanation of how they worked on the problem, others explained that they had prompted the children to devise hints that might 'un-stick' someone else.
Fran posed the question “where did you start and why?”:
• “The first one (3 squares multiplied together) stood out.” (Further questioning invited some consideration of cube numbers...)
• “The two last ones because I noticed the triangle in both, and then answer was a triangle, so I surmised it was zero.” (Further questioning about whether this could have been any other numbers instead? One?)
• “My class noticed the square number, green star also square and yellow semicircle must be a cube. So the children identified the type of number but not the actual number.”
The Teachers' Resources were shared, particularly the power point file, recording sheets and link to What's It Worth (extension activity). Flexibility was generally considered to be the most prevalent aspect of fluency for this task, due to the range of different approaches to the problem.
The last task used for the fluency in number section was Mystery Matrix, introduced with the prompt “Why are some numbers red and some black on the grid?” Participants were encouraged to discuss the structure on their tables.
Whilst working on the problem, Fran encouraged everyone to track their own 'pathway of progress' by putting letters into a second identical grid (A for the first cell completed, B for the second and so on.) Once colleagues had had time to try the activity for themselves, they were asked to compare their approach with someone else's - What was the same? What was different?
Participants discussed whether they had started in similar ways and then deviated, what different ways of tracking working might look like (an idea was suggested about having several grids and setting them out according to the starting points and route of progression) and took note of the extension interactivity Missing Multipliers.
After a break, Fran began session 2 by asking everyone to identify '3 wins' from their participation on the project so far as well as one area of challenge. Tables were grouped according to similar themes (the 9 identified at the start of the project), so that colleagues could share their thoughts in more detail. These themes yielded the following responses:
Enjoyment and engagement - You need to model the enjoyment!
Questioning - Have some key questions prepared e.g. How did you get started?
Vocabulary - We use a lot of displays in our classroom to support discussion, starters linked to the main activity to rehearse vocabulary, and a whole school document that builds on vocabulary year by year.
Greater Depth/differentiation/challenge - Our learners love being able to add their own creative stamp to their work and submit their solutions to NRICH (Fran signposted the orange box in the bottom middle of the new home page design to find recent Primary Solutions.)
Assessment, evidence and recording - Bringing approaches up from EY, focusing more on reasoning especially.
Confidence of staff and children - Repeated Heads and Feet, children more confident 2nd time around. Also allowing time to 'play' rather than going too quickly.
Resources linked to curriculum - Important to use NRICH curriculum maps and also important how they are used e.g. avoid only having problem solving on Fridays!
Following this, colleagues where given time to consider their planning for next steps to move on with the project, using their journals to reflect on their own steps for next year and to consider 3 ideas to contribute to next year's programme.
Feedback from each table as to what was going well and what was being worked on, was summarised on the posters shown below.


Referring to the four stages outlined by Wolfram (slide 13) of: posing questions, moving from the real world to a mathematical world with a model, doing the actual calculation, then moving from the mathematical model back to the real world; Fran showed a film of a growing number of counters 'dancing' on screen (animated factorisation diagrams). Participants were asked what questions they might pose for their pupils if the film were to be used as a prompt to developing creativity and curiosity in maths?
There is also a clip called Notes on a Triangle, which is part of Animated Triangles (in our Hidden Gems feature) which offers another video for similar purposes, with supporting teachers' notes.
Fran concluded by asking everyone to reflect on the Mathematical Mindsets book. Were there any particularly key chapters? And where else do you find reading to prompt/support mathematical discussion for staff and students? (Other than articles on NRICH!)
The afternoon's session 3, on fluency in statistics, began with Ems giving everyone 2 minutes to talk about the image below, prompting them with “What do you notice?”
When time had been allowed for discussion, Ems explained this was Florence Nightingale's contribution to statistics! She realised that visual ways of representing data would have more impact with politicians than tables of numbers and thus devised these polar area diagrams as a means of communicating the causes of mortality that were being faced in the Crimean War.
Another statistical representation called a Wagon Wheel was introduced, and Ems explained how both cricketers and air traffic controllers used these charts.
To introduce the task Olympic Records participants were asked to study the cards in their packs to see what they noticed. The clue that these were Olympic records for track and field events, was offered, together with the questions:
- How do you know?
- What can't it be?
- What questions do you have?
Cards with titles on were offered next, so that groups could check their conjectures when they were ready. There was much discussion and estimation going on, as well as speculation as to why some graphs were going up and down i.e. not showing an increasing or decreasing trend. (This turned out to be the result of a change in the number of points awarded per event in the decathlon and the
switch from a standing start to blocks in the 100m.)
Other anomalies expounded were:
• Some of the graphs starting later due to women not being allowed to take part in earlier games
• The javelin having it's weight altered in order to limit the distance thrown
• High jump records changing when the Fosbury Flop was introduced as a technique.
To continue on the sporting theme, the next task was Olympic Measures. The problem here is to match up numbers with their units and the category that both correspond to. Ems invited groups to check with each other or use their phones to verify that just one piece of information was correct, to act as an 'anchor'. Everyone was asked to
consider the strategies they used and then feedback:
• We started by categorising the data. Units were sorted into weights and lengths. The hardest part was allocating numbers, the units matched up quite well/straightforwardly.
• Quantifying something familiar e.g. something that I knew was that length.
• If I were to do this again I'd sort out those values which were whole numbers (I'm thinking the basketball hoop here) and decimal numbers for other categories.
• Reasoning is an important element - I did some checking by thinking “well I've got this one left and it can't possibly be that!”
• I'd be interested to ask learners which they found easier/harder and try and unpick why that was.
Next Sort the Street cards were given out to pairs, who were asked to sort them in a particular arrangement and then circulate to see how others had gone about it.
There was much shared surprise on discovering:
• Some people had used more than two groups
• Some had used more that two sorting criteria
• Some people had noticed things that others hadn't
• Some groupings were easier/harder to discern than others
Fran shared the idea from a teacher who asked her class to chose an interesting grouping and draw another house on a post it note to add to that configuration, to 'test out' their understanding.
Ems then challenged groups to use the post it notes on their tables to show as many different visual representations as possible. Ideas were shared at the front and then sorted into the following order given by the primary mathematics curriculum:
Y2 - Pictogram, tally chart, block diagrams, tables
Y3 - Bar chart
Y4 - Time graph
Y5 - Line graph, timetables
Y6 - Pie chart
The other suggestions of: Venn diagram, scatter graph, branch diagrams, sort diagram, Carroll diagram, box plot; are not actually mentioned in the primary curriculum.
However given their frequency of use as a statistical representation the problem Venn Diagrams has much to offer in developing fluency in statistics.
Ems explained that using Venn Diagrams in conjunction with Caroll diagrams can give a useful visual link between the 4 sections in each and help children see the data represented more clearly. The buzz in the room as participants worked on this task was palpable, as it was when nested Venn diagrams were alluded to, towards the very end of the session (a familiar flashback for Y6 teachers
from Test A in 2012!)
The Department for Education (July 2016) states that:
“Effective teacher professional development is a partnership between:
• Head teachers and other members of the leadership team;
• Teachers; and
• Providers of professional development expertise, training or consultancy.
In order for this partnership to be successful:
1. Professional development should have a focus on improving and evaluating pupil outcomes.
2. Professional development should be underpinned by robust evidence and expertise.
3. Professional development should include collaboration and expert challenge.
4. Professional development programmes should be sustained over time.
And all this is underpinned by, and requires that:
5. Professional development must be prioritised by school leadership.”
In supporting delegates to attend 6 days of training over the course of 2016-17 school leaders in Tower Hamlets have shown that they value the professional development of their staff. In designing the programme, NRICH undertook to align the provision with the other 4 criteria and 94% of the teachers we worked with, (who completed surveys at the beginning and end of the project,) reported an
increase in their own and their class' confidence to mathematically problem solve by the end of the school year.
Thank you to Tower Hamlets LA for commissioning this project and to all those teachers who contributed to the exchange of ideas and created a supportive and professional climate in which it was possible to experiment and explore together.
2017-18 programme dates:
Wednesday 4th October
Wednesday 29th November
Tuesday 9th January
Tuesday 6th March
Wednesday 18th April
Wednesday 20th June