Rohan from Wilson’s School in England and Sowjanya, Avyukt, Taran, VinamaraSai, Niveditha, Adhrit, Sara, Achyuth, Abheer, Kavicharan, Agasthya, Pranit, Riddhit and Eshaan (with Shubhangee) from Ganit Kreeda, Vicharvatika in India investigated the number of moves needed when there are the same number of red and blue frogs. Shubhangee wrote:

We explored to find minimum number of moves to swap with different number of frogs using interactivity. Strategy we used to swap pink frogs (on left) with blue frogs (on right) in minimum number of moves without moving backward was:

• No same coloured frog will come back to back.
• Always create a gap between two same coloured frogs, so that the other coloured frog can jump/ slide to fill the gap.

Rohan added some more advice:

From experimenting with red and blue frogs, I concluded that you could always swap the frogs over without moving any frogs backwards. The key thing to remember was that an alternating pattern of red and blue frogs should be maintained whilst moving the frogs.

Shubhangee’s students then recorded the minimum number of moves in a table. These are Niveditha’s recordings:

Here are Agastya and Pranit’s observations:

Here are Taran’s recordings:

Rohan continued this approach:

I realised that the change in moves were all odd numbers and increased in increments of 2. From this, I could create a formula to predict the number of moves required using n as the number of blue or red frogs (since, in this instance, they are equal): No. of moves $= n^2 + 2n$

VinamaraSai, Adhrit and Avyukt’s recorded the moves:

Moves recorded as Pink(P) and Blue(B) Frogs:
P
BB
PPP
BBB
PPP
BB
P

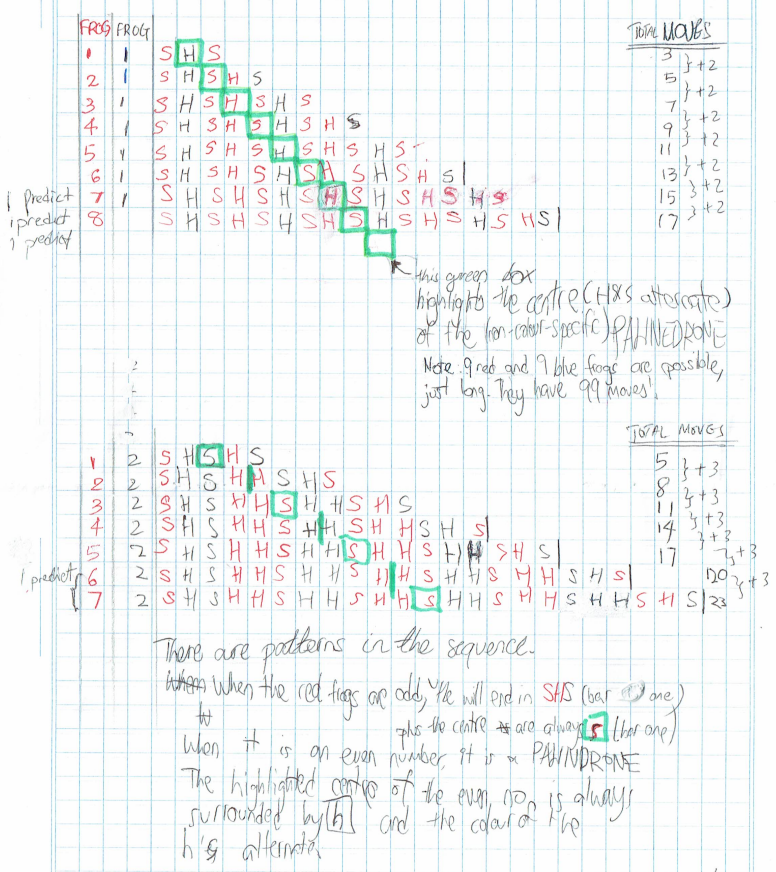
Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Australia and Sowjanya, Sara and Achyuth used S to represent a Swipe and H to represent a Hop. This is Sowjanya, Sara and Achyuth’s work which begins by using four frogs of each colour.

It can be further generalized for $n\times n$ frogs as:

No. of moves $= 1+2+3+---+n+n+n+---+3+2+1$

No. of moves $= \frac{n(n+1)}{2} + n + \frac{n(n+1)}{2}$

No. of moves $= n(n+1) + n$

No. of moves = $n^2 + 2n = n(n+2)$

Can you see how all the formulas above mean the same thing?

Daya from Hutchesons’ Grammar School in the UK, Yu-Tong from Colyton Grammar School in England, Rohan and Ci Hui Minh Ngoc Ong experimented with different numbers of red and blue frogs. Daya and Ci Hui Minh Ngoc started with just one frog of one colour. Daya wrote:

I found a pattern between numbers with having a certain amount of frogs on 1 side and just one frog on the other side. I went up by one each time, so I started with 1,1 and got 3 moves, each time I added another number to the left side the amount of moves increased by 2. When I did 2,1 I got 5 moves and they kept on increasing by 2 each time.

This is Ci Hui Minh Ngoc Ong’s work (click to enlarge):

Rohan tried using one more frog of one colour than the other, and then two more, and so on:

Yu-Tong found the same formula, but wrote it in a different and more general way:

The number of red frogs multiply by the number of blue frogs equals the number of jumps and if you add the number of the two different coloured frogs it will equal the number of slides so the formula would be rb+r+b to get the number of moves if r represents the number of red frogs and b represents the number of blue frogs.

Yu-Tong’s method is below, but thnk about why the number of jumps is equal to $b\times r$, and why the number of slides is equal to $b+r$ - or one slide per frog. If you are already convinced that the frogs can always move into their final position without going backwards, is this enough to convince you that this forumla must be correct?

Yu-Tong’s method:

At first I used 2 red frogs and 2 blue frogs and the number of moves were 8 and 3 frogs of each colour and got 15. I noticed that 2 red frogs multiplied by 2 blue frogs then doubled would get 8. However this did not work for 3 red and 3 blue frogs so I tried to but it in another way. I found that another way was 2(2+2) and this would also give the answer 8 so I tried the method of 3 red and 3 blue frogs and it got me the answer 15. After many tries I came to a conclusion that with the same number of frogs on each side the method{2(2+2) = a(a+a)} works so then I tried it on an occasion when the number of frogs aren't the same.

When I tried 2 red frogs and 3 blue frogs I found out that either way it would be one less or one too more. From this I figure out that this equation a(a+a) is the same as a*a+a+a and if the numbers are different then it would be a*b+a+b. The main methods used was first looking for a pattern that I wrote it in algebra and then expanded it to get the solution.