Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Polygon Rings
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
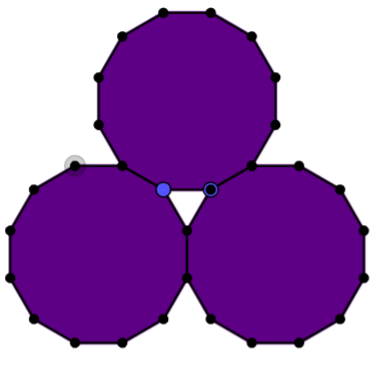
Letizia from Bangkok Patana School in Thailand, Rose from Channing School in the UK, Caroline, Marcos and Jayne from Kings' School Al Barsha in UAE and Alex from Leighton Park School in the UK worked out how many pentagons form a ring.
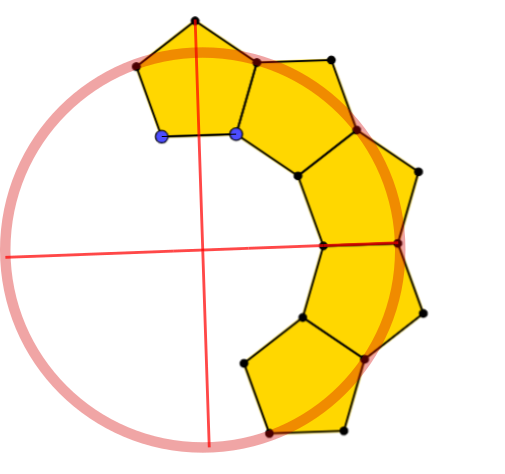 Marcos used the diagram to imagine a full ring:
Marcos used the diagram to imagine a full ring:Well if you were going to think of a circle you can divide it into 4 equal sizes in one of the is equal to two pentagons and a half. If you add all is equal to a loop full of pentagons [which makes 10 pentagons].
Letizia and Rose used the interactivity to make full pentagon rings. This is Rose's ring:

Norawee from King Georve V School in Hong Kong and Alex used angles to explain why 10 pentagons make a ring without overlapping.
Below is Alex's explanation and diagram.
Click here to see Norawee's work, which goes into more depth than Alex's.
Because the ring is made out of regluar pentagons, we can work out that each of the interior angles of each pentagon is 108* degrees. By extending the lines that two pentagons share, assuming they will all meet in the middle, it will create a triangle.
As we know each angle of a [regular] pentagon is 108* degrees, we know the two base angles of the triangle would equal to 72** which leaves the top angle to be 36 degrees.
As [the sum of] angles at a point is 360 degrees, and 36 is divisible by 360, it will make a complete ring.
Also, as 360 ÷ 36 = 10, we know that the ring will be made out of 10 pentagons.
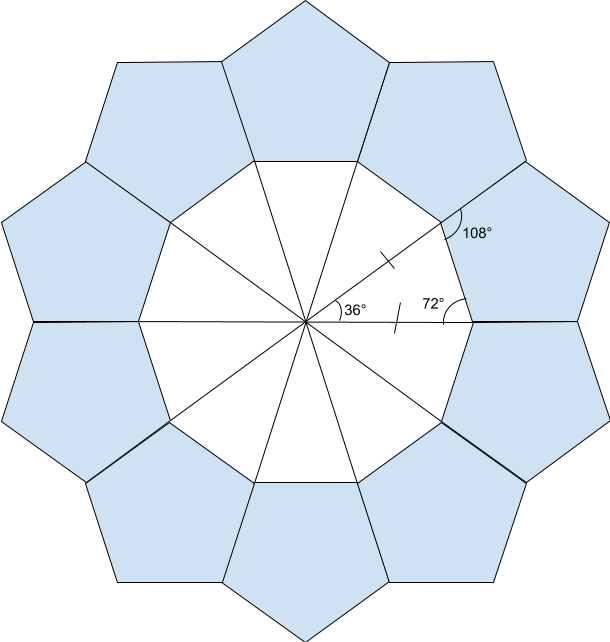
Pentagons above are regluar pentagons.
*as formula to calculate the the size of a interior angle of a polygon is $(n \times 180 - 360) \div n$ (for $n$ being the number of sides that the polygon has).
**because the triangle is made by extending the lines, and angles on a line is $180$ degrees, $180 - 108$ (an interior angle of a pentagon) $= 72.$
Caroline said 5 decagons would form a ring, and Jayne said 10 decagons would form a ring. Letizia said 5 decagons would form a ring, but sent in this picture of 10 decagons in a ring (left). On the right is a ring made from 5 decagons.
In the 10-decagon ring, the shape in the middle uses 3 sides from each decagon. In the 5-decagon ring, the shape in the middle uses 2 sides from each decagon.
If we force the shape in the middle use only 1 side of each decagon (like we did with the pentagons), then decagons cannot form a ring, because they overlap:
Which polygons can make rings around a shape which uses only 1 side of each polygon?
Pinyo from Thailand, Mimi, Denis, Jomkwan and Jessica from Headstart International School Phuket in Thailand and Iqra from Uphall Primary School in the UK sent answers to this question. Here is Jessica's work:
In a polygon ring, some particular polygons can form a ring with another polygon inside of it. Not all polygons can do this. The only weird thing about it is that the shape inside the ring has to only use one of the exterior sides.
Hexagon (6-gon)
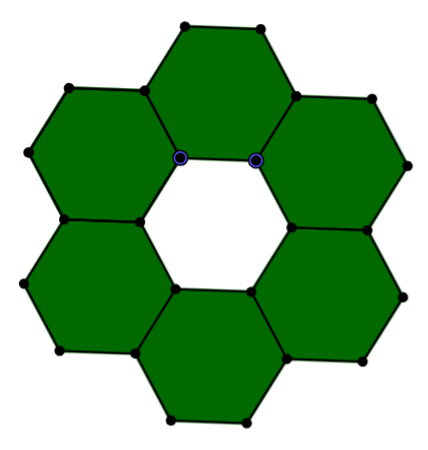
We can seein the hexagon ring is that the shape that has formed on the inside of the ring is a hexagon. In this diagram, one side of the shape is used to make the inside shape.
Octagon (8-gon)
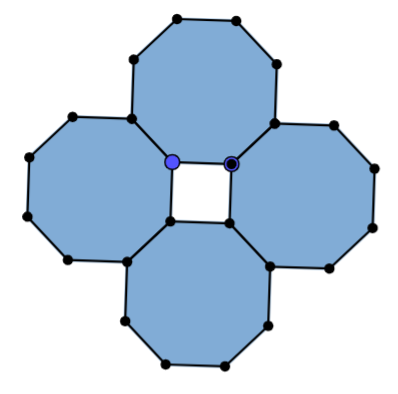
In this octagon, 4 put side by side made a square in the middle. Therefore this fits my investigation on polygon rings.
Dodecagon (12-gon)
In this dodecagon, 3 of each shape was used to make a polygon in the middle. As we can see the shape is a triangle and only used 1 side of each shape.
You can also use squares to make a ring. I used 12 squares but you can make it as big as you want.
Daniel from Moor End Academy in the UK and Mimi looked at the angles of the polygon which is formed in the middle. This is Daniel's work:
There are only regular polygons being used, so we can assume that the interior angle of every [polygon] used in the diagram [is] $\dfrac{(n-2) \times 180}n$
Where two regular [polygons] connect, the sum of the two interior angles, and $x$ (where $x$ the interior angle of the polygon in the middle), is equal to $360.$
When solving the equation $2\times \dfrac{(n-2) \times 180}n + x = 360$, we find $x$.
We should find the exterior angle to find the amount of sides. We do this by taking [$x$] away from $180$.
When we divide $360$ by [the exterior angle], we get the number of sides the polygon in the center has.
The final equation for how to make a ring out of any shape is: $$\frac{360}{-180+\left(\frac{(n-2)\times360}n\right)}=\text {sides, or number of polygons needed}$$
The denominator can be written as:$$\begin{split}-180+\left(\dfrac{(n-2)\times360}n\right)&=\dfrac{-180n}n+\dfrac{(n-2)\times360}n\\
&=\dfrac{-180n+360n-720}{n}\\
&=\dfrac{180(n-4)}{n}\end{split}$$
Which means the formula for the number of sides can be rewritten as:$$\begin{split}\text{sides, or number of polygons needed}&=\frac{360}{-180+\left(\frac{(n-2)\times360}n\right)}\\
&=\frac{360}{\frac{180(n-4)}{n}}\\
&=\frac{360n}{180(n-4)}\\
&=\frac{2n}{n-4}\end{split}$$
Florence from Walthamstow Hall Junior School pointed out that this must be a whole number. This is enough to find how many different rings there are:
$s=\frac{2n}{n-4}\Rightarrow s(n-4)=2n$
| $s$ | formula for $n$ | possible? |
| $3$ | $3(n-4)=2n\\ 3n-12=2n$ |
$n=12$ (seen) |
| $4$ | $4n-16=2n\\ 2n=16$ |
$n=8$ (seen) |
| $5$ | $5n-20=2n\\ 3n=20$ |
no |
| $6$ | $6n-24=2n\\ 4n=24$ |
$n=6$ (seen) |
| $7$ | $7n-28=2n\\ 5n=28$ |
no |
| $8$ | $8n-32=2n\\ 6n=32$ |
no |
| $9$ | $9n-36=2n\\ 7n=36$ |
no |
| $10$ | $10n-40=2n\\ 8n=40$ |
$n=5$ (seen) |
- $s$ can't be smaller than $3$ so the dodecagons are the largest polygons which can form a ring (around a triangle)
- Continue searching using $n$ since below $5$, $n=3$ or $n=4$
| $n$ | $s=\frac{2n}{n-4}$ | comment |
| $4$ | division by zero | This fits with Iqra's observation that you can use as many squares as you like |
| $3$ | negative | In fact triangles do make a ring, but there is no shape in the middle |
Which polygons can make rings around shapes which use more than 1 side of each polygon?
Mimi found the following polygon rings:
5 decagons use 2 sides each, 10 decagons use 3 sides each, 14 heptagons use 3 sides each, 18 nonagons use 3 sides each, 22 hendecagons use 4 sides each.