 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Next Number



Lisa and Alana from Sudbourne School, Lambeth used words to explain how they worked out the next number:
The answer to what is the next number is $163$ because the difference between $3$ and $7$ is $4$ and the next difference (between $7$ and $19$) is $12$ which is $3 \times 4$. The difference after that (between $19$ and $55$) is $36$ which is $12$ (the last difference) times $3$ (the first number, also the number timsed by $4$ to get $12$.) So we just added $108$ to $55$ which equals $163$.
Sinan from IRMAK Primary School, Istanbul, Turkey says much the same thing with numbers:
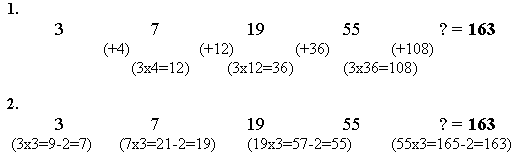
Sarah from Annesley College, Adelaide South Australia explained it a slightly different way:
I figured it out by working out how much the difference is between the four numbers. Then I found that all the numbers between are all factors of three. So, I times each of the between numbers by three. When I got to $55$ times three I got $108$. Then I added $55$ and $108$ and I got $163$. This was the answer I got.
Shivana from Henry Park Primary School, Singapore has another way of writing it:
The answer is $163$: $n \times 3 - 2$ ($n$ being the previous number).
Example $19 \times 3 - 2 = 55$
Emir from IRMAK Primary School, Istanbul, Turkey worked it out in a similar way.
The following people also explained their thinking quite well:
Laura from St Ives School, Haslemere.
Ruyi from Annesley College, Adelaide South Australia
Alex from The Abbey, Woodbridge, Suffolk
Jason from Priory School
Ruth and Jessica from St Lawrence Primary School, Lechlade.
Jenny, Emily, Caroline, Natalie and Rebecca from The Mount School York
Kathryn, Katerina, Nicola and Andrew from Primary Maths Club, International School of Toulouse.
Leyla, Gizem, Unal, Melis, Huma, Ece, Idil, Gizem, Alta, Ece, Simin, Eda S, Ece O, Cana, Sinan, Melike, Efsane, Emre, Ilayda, Baran fromIRMAK Primary School, Istanbul, Turkey.
Thomas and Justin from Tatingstone School
Michael from St Francis Catholic Primary, Essex
Christina from Malborough Primary
And finally, a short neat explanation from Steven from Burpham Primary School, Guildford, Surrey:
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.