Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Age 11 to 18
Published 2013 Revised 2018
Problems We Wish Were on NRICH
Over the past year, we have been inspired by Nrich and the type of mathematical tasks it uses. Throughout our placements we have all used both Nrich problems and our own problems of an Nrich style which we believe are worthy of being on Nrich. This article will present some of these problems and explains our rationale for why they should be included on Nrich.
Problem 1 - The Monty Hall Problem
This problem is based on the game show where there are three doors. Behind two doors are goats and behind the other is a car. The host asks you to pick one of the three doors. After you have picked a door, the host will open one of the doors you did not pick to reveal a goat. You are then asked if you wish to switch your choice to the other unopened door or
stick with the one you already chose with the question being, 'what will maximise your chance of finding the car?' Of course, this assumes that everyone wants to find the car rather than a goat!
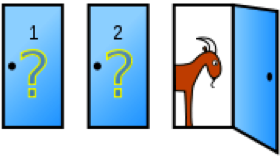 This problem is worthy of NRICH as it is counter-intuitive; most would assume it is of no advantage to switch doors but
mathematically it is. This could allow for a lot of debate, discussion and reasoning in the classroom. The problem uses aspects of conditional probability and can be solved by drawing tree diagrams and calculating probabilities of successive
events.
This problem is worthy of NRICH as it is counter-intuitive; most would assume it is of no advantage to switch doors but
mathematically it is. This could allow for a lot of debate, discussion and reasoning in the classroom. The problem uses aspects of conditional probability and can be solved by drawing tree diagrams and calculating probabilities of successive
events.
Problem 2 - The Josephus Problem
 In 67 AD, Josephus Flavius, commander of Galilee and 40 of his soldiers were besieged in a cave by a Roman army. Rather than be captured, the 41 warriors decided to end their own lives. According to legend, the soldiers formed a circle and numbered themselves from 1 to 41. Starting with person 2, they killed every
alternate person, by passing a sword around the circle, until no-one remained. Josephus worked out where he should stand to survive. How did he do this?
In 67 AD, Josephus Flavius, commander of Galilee and 40 of his soldiers were besieged in a cave by a Roman army. Rather than be captured, the 41 warriors decided to end their own lives. According to legend, the soldiers formed a circle and numbered themselves from 1 to 41. Starting with person 2, they killed every
alternate person, by passing a sword around the circle, until no-one remained. Josephus worked out where he should stand to survive. How did he do this?This problem is Nrich worthy as it allows pupils to work systematically by trying different group sizes to find patterns. They can then generalise to give the position for the last remaining person for any group size. At the same time pupils will use their knowledge of powers of two and can consider binary notation. The problem can also be extended to skipping different numbers of people.
Problem 3 - The Hat Game
 Imagine there are 100 pieces of paper in a hat, labelled from 1-100. Two pieces of paper are chosen at random. The smaller number is subtracted from the larger number and the answer is written on a new piece of paper. This number is placed back in the hat and the two original numbers discarded.
The process repeats until one number is left. What can you say about the final number left in the hat?This problem allows pupils to try smaller amounts of numbers in the hat and see if they find a pattern from which they can generalise. They will look at different combinations of even and odd numbers and see what happens.
Imagine there are 100 pieces of paper in a hat, labelled from 1-100. Two pieces of paper are chosen at random. The smaller number is subtracted from the larger number and the answer is written on a new piece of paper. This number is placed back in the hat and the two original numbers discarded.
The process repeats until one number is left. What can you say about the final number left in the hat?This problem allows pupils to try smaller amounts of numbers in the hat and see if they find a pattern from which they can generalise. They will look at different combinations of even and odd numbers and see what happens.
Problem 4 - The Tower Challenge (problem from www.suffolkmaths.co.uk)
 The challenge is to design a tower consisting of three blocks, a trapezoidal prism, a cuboid and a triangular prism, subject to some constraints. Each block must have a volume of 1000$cm^3$, the 3 blocks must meet perfectly with no overhang, the minimum dimension allowed is 5cm and the area of
the base must be at least 5 times bigger than the horizontal width of the tower. The challenge element is to maximise the height of the tower.This problem allows pupils to practise finding the volume of many different prisms without being given a sheet of questions to work through. It also allows them to consider factors of 1000 and combinations of these
which work with the formulae. It is similar to some of the existing Nrich problems including Cuboids and The Cuboid Challenge.
The challenge is to design a tower consisting of three blocks, a trapezoidal prism, a cuboid and a triangular prism, subject to some constraints. Each block must have a volume of 1000$cm^3$, the 3 blocks must meet perfectly with no overhang, the minimum dimension allowed is 5cm and the area of
the base must be at least 5 times bigger than the horizontal width of the tower. The challenge element is to maximise the height of the tower.This problem allows pupils to practise finding the volume of many different prisms without being given a sheet of questions to work through. It also allows them to consider factors of 1000 and combinations of these
which work with the formulae. It is similar to some of the existing Nrich problems including Cuboids and The Cuboid Challenge.
Problem 5 - Efron's Dice
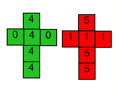
This involves four different coloured dice which are not numbered in the standard way. Two dice are rolled and the highest number rolled wins. The task is a probability one, if one player chooses a die, which die should you choose in order to maximise your chance of beating that die?
This task allows pupils to consider different combinations of outcomes
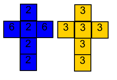 by drawing up sample spaces and probabilities trees. They then consider probabilities of independent events and mutually exclusive outcomes in order to solve the problem. They should discover an interesting property of these four dice.
by drawing up sample spaces and probabilities trees. They then consider probabilities of independent events and mutually exclusive outcomes in order to solve the problem. They should discover an interesting property of these four dice.
Problem 6 - The Bean Game
 This is a two player game involving a pile of 23 beans. The players successively remove beans from the pile taking 1, 2, 3 or 4 at a time. The aim is to find a winning strategy which allows the first player to always guarantee winning.
This is a two player game involving a pile of 23 beans. The players successively remove beans from the pile taking 1, 2, 3 or 4 at a time. The aim is to find a winning strategy which allows the first player to always guarantee winning.In this problem pupils will consider partitions of numbers, whilst practising their basic arithmetic skills and looking at multiples of numbers. The problem can be extended by looking at different sized piles, taking different amounts from each pile or having multiple piles.
Problem 7 - The Taxman Game
 A two player game, involving a grid of numbers from 1 to 30. The first player picks a number and adds it to their list. However, the second player will receive all the factors of this number in their list. All these numbers in the grid are then crossed off and player two takes a go. At each
stage, all remaining factors are added to the other player's list. This continues until all numbers are crossed off the grid. The aim is to end up with the highest total when adding up all the numbers in the list.The problem allows pupils to develop a strategy which they can refine over multiple plays. The game should stimulate classroom discussion on
strategies about which numbers are good to pick or not. Pupils will be able to consider factors of numbers and why some numbers have more factors than others.
A two player game, involving a grid of numbers from 1 to 30. The first player picks a number and adds it to their list. However, the second player will receive all the factors of this number in their list. All these numbers in the grid are then crossed off and player two takes a go. At each
stage, all remaining factors are added to the other player's list. This continues until all numbers are crossed off the grid. The aim is to end up with the highest total when adding up all the numbers in the list.The problem allows pupils to develop a strategy which they can refine over multiple plays. The game should stimulate classroom discussion on
strategies about which numbers are good to pick or not. Pupils will be able to consider factors of numbers and why some numbers have more factors than others.
Problem 8 - Bish, Bash, Bosh
 This could be done in pairs or as a whole class activity. Players consecutively count from 1 upwards except when a multiple of 3 is reached you say bish and when a multiple of 5 is reached you say bash. If the number is a multiple of both 3 and 5 you say bosh instead.Pupils can
think about the pattern generated and which numbers will be bosh numbers. The game also nicely leads onto a discussion of Lowest Common Multiples. The game could also be played with numbers other than 3 and 5 and could be done with those in the same times table e.g. 4 and 8 which could lead to some interesting discussion.
This could be done in pairs or as a whole class activity. Players consecutively count from 1 upwards except when a multiple of 3 is reached you say bish and when a multiple of 5 is reached you say bash. If the number is a multiple of both 3 and 5 you say bosh instead.Pupils can
think about the pattern generated and which numbers will be bosh numbers. The game also nicely leads onto a discussion of Lowest Common Multiples. The game could also be played with numbers other than 3 and 5 and could be done with those in the same times table e.g. 4 and 8 which could lead to some interesting discussion.Problem 9 - Kaprekar Numbers
 Take four digits from 0-9 and arrange them to make the biggest four digit number possible and also the smallest four digit number. Subtract the smallest from the largest to get a new 4 digit number. Rearrange this 4 digit number to give its smallest and largest, and keep repeating. See if anything
happens.
Take four digits from 0-9 and arrange them to make the biggest four digit number possible and also the smallest four digit number. Subtract the smallest from the largest to get a new 4 digit number. Rearrange this 4 digit number to give its smallest and largest, and keep repeating. See if anything
happens.This process allows pupils to practise their skills of subtraction as well as pattern finding and attempting to explain their results. It can also be extended to numbers of different length for pupils to continue to explore.
Problem 10 - Wrong + Wrong = Right
 The task is to find out what the letters could stand for in the addition on the right to make it true.
The task is to find out what the letters could stand for in the addition on the right to make it true.The problem allows pupils to practise their skills of adding large numbers together without giving them a page of sums to do. It allows them to use reasoning and logic to decide which letters could be certain numbers and which could not. This could be done by looking at carrying and looking at numbers which repeat. As an extra challenge pupils could be asked to find all the possible 5 digit numbers which work.
Problem 11 - Drink Mixing (based on a problem on Dara Ó Briain's School of Hard Sums)
 Imaging you have a glass of white wine and a glass of red wine, each of the same volume. You remove a shot of red wine and pour it into the white wine and then remove a shot from this mixture and pour it back into the red wine. The question is, is there more red wine in the white wine glass or more white wine in the
red wine glass?
Imaging you have a glass of white wine and a glass of red wine, each of the same volume. You remove a shot of red wine and pour it into the white wine and then remove a shot from this mixture and pour it back into the red wine. The question is, is there more red wine in the white wine glass or more white wine in the
red wine glass?This problem allows pupils to look at fractions and ratios and find a strategy to work out the problem. It could allow for a lot of debate and discussion in the classroom as pupils try to defend their answer to quite a counter-intuitive problem.
”ƒ
Problem 12 - The Condemned Man
 A man has been sentenced to execution but is given one last chance by the judge. The judge gives him two stone urns and fifty black balls and fifty white balls. The man is told that he has to arrange the balls in the two stone urns overnight and in the morning the judge will pick an urn at random and then remove a
ball from that urn at random. If the ball is white the man will be set free and if black he will be executed. Is there a way the balls can be arranged so the man can have a greater than even chance of being freed?
A man has been sentenced to execution but is given one last chance by the judge. The judge gives him two stone urns and fifty black balls and fifty white balls. The man is told that he has to arrange the balls in the two stone urns overnight and in the morning the judge will pick an urn at random and then remove a
ball from that urn at random. If the ball is white the man will be set free and if black he will be executed. Is there a way the balls can be arranged so the man can have a greater than even chance of being freed?This problem allows pupils practise at drawing probability trees, specifically what needs to go on the branches, and using them to calculate probabilities of successive events and mutually exclusive events. It also allows them to develop a strategy and try to refine it as they progress towards deciding whether there is a solution or not.
Problem 13 - Dim Sum Problem (based on a problem on Dara Ó Briain's School of Hard Sums)
 Imagine you are in a restaurant in China where nobody speaks English and the menu is all in Chinese. There are 9 items on the menu but you have no idea what they are. You can order 5 dishes at a time (with repeats of the same dish in each order allowed). What is the minimum number of times you will need to order to
be able to establish which dish is which on the menu?
Imagine you are in a restaurant in China where nobody speaks English and the menu is all in Chinese. There are 9 items on the menu but you have no idea what they are. You can order 5 dishes at a time (with repeats of the same dish in each order allowed). What is the minimum number of times you will need to order to
be able to establish which dish is which on the menu?This problem allows pupils to look at combinations and use their reasoning and logic to be able to work out what they know from a certain order. Pupils can also look at different numbers of items on the menu and the ability to order different numbers of items at a time to see if they can find a pattern to explain.