Face painting
Problem
Here is a picture of the five Platonic solids:
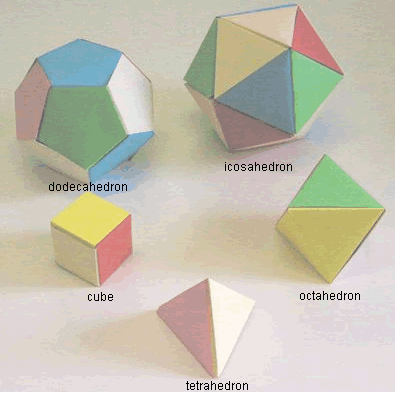
Imagine you want to make each of the five Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Can you find the least number of colours for which this is possible for each polyhedron.
How did you go about finding your solutions?
If you'd like to make these solids out of paper, have a look at Ian Short's article.
Getting Started
How many other faces does each face touch?
Have you tried drawing a net of the shape?
It might help to make the shape out of Polydron, or perhaps you can find some solid shapes to work with?
Student Solutions
We received this solution from someone who didn't give their name:
In a tetrahedron any two faces have a common edge so no two faces can be the same colour. A tetrahedron needs 4 colours. If we start by colouring one face, then the 3 faces adjoining it need 3 more colours.
A cube needs at least 3 colours because 3 faces meet at a point. Three colours are sufficient because each pair of opposite faces can be painted in one of the 3 colours.
An octahedron needs 2 colours. At each vertex 4 faces meet and they can be painted in alternate colours.
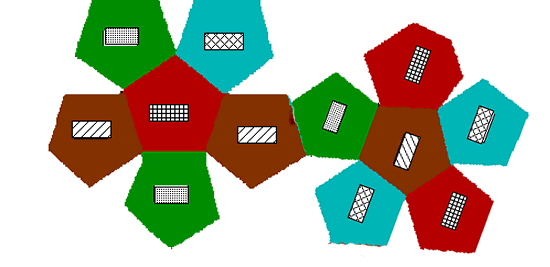
A dodecahedron needs at least 4 colours because if we start by colouring one face then we have to use 3 more colours to paint the faces around it. The net shows how the dodecahedron can be painted with 3 faces of each colour so 4 colours are sufficient.
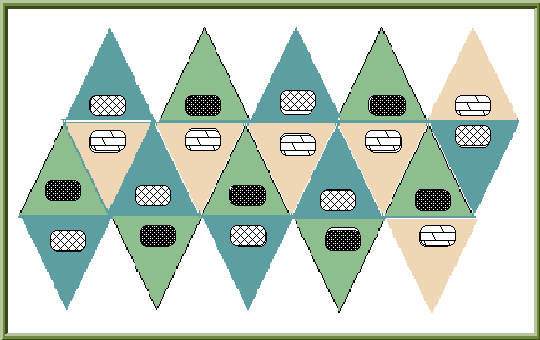
An icosahedron needs at least 3 colours because we have to use 3 colours to paint the 5 faces around each vertex. Three colours are sufficient as shown in the net.