Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Resources tagged with: Odd and even numbers
There are 7 results
Broad Topics > Properties of numbers > Odd and even numbers
Article
Primary curriculum
Secondary curriculum

Impossible Sandwiches
In this 7-sandwich: 7 1 3 1 6 4 3 5 7 2 4 6 2 5 there are 7 numbers between the 7s, 6 between the 6s etc. The article shows which values of n can make n-sandwiches and which cannot.
Age 11 to 18
Article
Primary curriculum
Secondary curriculum

Modulus Arithmetic and a Solution to Differences
Peter Zimmerman, a Year 13 student at Mill Hill County High School in Barnet, London wrote this account of modulus arithmetic.
Age 16 to 18
Problem
Primary curriculum
Secondary curriculum
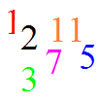
Prime Magic
Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?
Age 7 to 16
Challenge Level 





Problem
Primary curriculum
Secondary curriculum
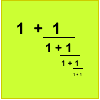
Comparing Continued Fractions
Which of these continued fractions is bigger and why?
Age 16 to 18
Challenge Level 





Problem
Primary curriculum
Secondary curriculum

Summats Clear
Find the sum, f(n), of the first n terms of the sequence: 0, 1, 1, 2, 2, 3, 3........p, p, p +1, p + 1,..... Prove that f(a + b) - f(a - b) = ab.
Age 16 to 18
Challenge Level 




