At a glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Problem
Image

The area of a regular pentagon looks about twice as a big as the pentangle drawn within it.
Is it?
Student Solutions
Image
Congratulations to all the following who sent in very good solutions to this problem: David from Trinity School, Carlisle (whose solution was the first to arrive); Babak Shirazi from Woodhouse SF College, London; Chen Yiwen from The Chinese High School, Singapore; Nathan from Riccarton High School, Churchtown, New Zealand; Lee Jia Hui from National Junior College, Singapore and finally Alexander from Shevah-Mofet School, Israel. The following solution is made up of bits supplied by several of these contributors.
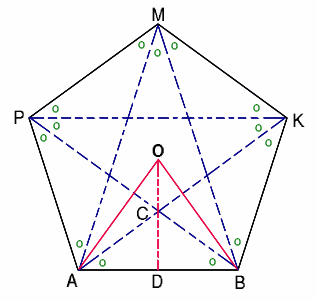
The pentagon is made of 5 triangles exactly the same as $AOB$, and the pentangle is made of 5 shapes exactly the same as $AOBC$.
\begin{eqnarray} \\ \frac{{\rm Area
(pentangle)}}{{\rm Area (pentagon)}} &=& \frac{{\rm Area
(AOBC)}}{{\rm Area (AOB)}}\\ &=& 1-\frac{{\rm Area
(ACB)}}{{\rm Area( AOB)}} \\ &=& 1-\frac{{\rm Area
(DCB)}}{{\rm Area (DOB)}} \\ &=& 1-\frac{DC}{DO}\\
&=& \frac{CO}{DO} < \frac{1}{2}. \end{eqnarray}
In order to calculate this ratio exactly we first find the angles
and then use trigonometry. $$ \angle AOB = 72^\circ $$ $$\angle DOB
= \frac{1}{2}\angle AOB = 36 ^\circ $$As $AC$ is parallel to $PM$
and $CB$ is parallel to $MK$, $$\angle ACB = \angle PMK = 108
^\circ . $$ $$\angle DCB = {1\over 2}\angle ACB = 54^\circ .$$
\begin{eqnarray} \\ \frac{{\rm Area
(pentangle)}}{{\rm Area (pentagon)}} &=& 1-\frac{DB \tan
36}{DB\tan 54}\\ &=& 1-{\tan 36 \over \tan 54} \\
&=& 1- \tan^2 36 \\ &=& 1- (5 - 2{\sqrt 5}) \\
&=& 2{\sqrt 5} - 4 \\ &=& 0.47\quad {\rm approx.}
\end{eqnarray}
This ratio is just less than 0.5 meaning the pentangle is a bit
smaller than half the pentagon.Footnote: You don't need a calculator, from the diagram it is possible to calculate exact values for the trig. ratios for $18^\circ $, $36^\circ$, $54^\circ$ and $72^\circ$. All the angles marked with a spot can be shown to be $36^\circ$ using simple properties of triangles. Let $CA=CB=x$. The triangle $PAC$ is an isosceles triangle with base angles of $72^\circ$. If $PA=PC=1$ then $PB=1+x$. Triangles $PAB$ and $ACB$ are similar, hence $$\frac{x}{1} = \frac{1}{1+x}$$
This gives a quadratic equation which can be solved to give $x = \frac{1}{2}({\sqrt 5} - 1).$
Now we have $AD={1\over 2}$ and so (using Pythagoras Theorem to find $CD$): $$\tan^2 36^\circ = 4CD^2 = 4(x^2 - \frac{1}{4}) = 4x^2 - 1 = 5 - 2{\sqrt 5}.$$
