Whirlyball

Andrei from Tudor Vianu National College, Bucharest, Romania and Shaun from Nottingham High School both sent in excellent solutons to this problem.

 

Image

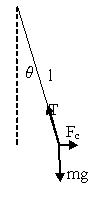
After drawing the picture, I observed that the forces (the gravitational force acting on the ball, the tension in the wire and the centrifugal force) keep the body in equilibrium. Considering the centrifugal force, I work in a non-inertial frame of reference, i.e. in the frame centred on the ball, which is in an accelerated movement in respect to Earth.   In terms of the vectors we have $$m g +  F_c + T = 0.$$

Resolving horizontally and vertically and using $F=ma$ (where $a$ is the acceleration towards the centre and $T$ is the magnitude of the tension in the string):

$$

\begin{align}

T\cos \theta &= mg\\

T\sin \theta &= ml\sin \theta \omega^2\;.

\end{align}

$$

Eliminating $T$: $$l\omega^2 \cos \theta = g$$ and hence the angle $\theta$ is $\cos^{-1}{g\over l\omega^2}$.

I know that $\cos^{-1}$ is a decreasing function in the interval of interest for the problem. As $\omega$ increases, the angle $\theta$ also increases and the whirling ball rises up, the radius of its circular path also increasing.

The ball can whirl in a circle while $\theta > 0$. So, as I explained above, to find the smallest angular velocity, I have to find the smallest angle. For $\theta \to 0$, ${g\over l\omega^2}\to 1$ and so $$\omega \to \sqrt {g\over l}.$$ This is the smallest angular velocity with which the ball could rotate in a circle.

The period of this movement is: $$T = {2\pi \over \omega} = 2\pi \sqrt {l\over g}.$$ It is interesting to observe that this is also the period of isochronal oscillations of the mathematical pendulum, i.e. the period of oscillation of a material point of mass $m$ attached to an inextensible string without mass deviated from the vertical by angles less than $5^\circ$.