Walk Up the Escalator

Answer: 36 seconds

Using proportion

Still on moving escalator, travel 1 escalator in 60 seconds = $\frac1{60}$ escalator per second

Walking on still escalator, travel 1 escalator in 90 seconds = $\frac1{90}$ escalator per second

Walking on moving escalator, travel $\frac1{60}+\frac1{90}$ escalator per second

                                                $=\frac{3}{180}+\frac2{180}$

                                                $=\frac5{180}$

                                                $=\frac1{36}$ escalator per second = 1 escalator in 36 seconds.

Using a distance-time graph

Length of escalator is $d$.

Image

 

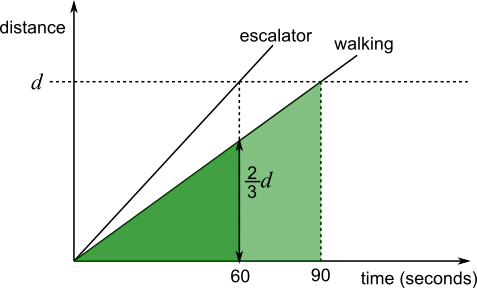
Walking up the moving escalator: add the distances.

If Aimee walks for $60$ seconds walks up the escalator, she travels $d+\frac{2}{3}d=\frac53d$

Image

 

 

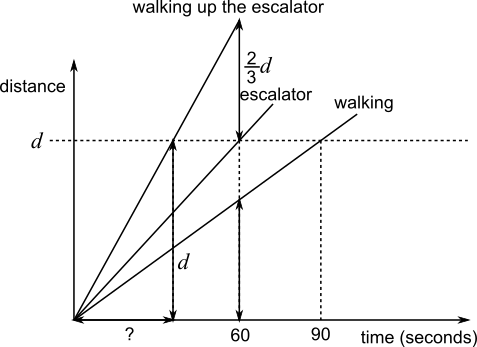
   $\frac53d$ in $60$ seconds

$=5d$ in $180$ seconds

$=d$ in $36$ seconds

Using algebra and the speed-distance-time relationship

Escalator travels with speed $a$

Aimee walks with speed $b$

When Amy walks up the moving escalator, she has speed $a+b.$

distance = speed $\times$ time, so the length of escalator is given in 3 ways: $$60a=90b=(a+b)t$$

Aim: find $t$ (which might involve also finding $a$ and $b$)

Notice we have $(a+b)\times t$ so could get $t$ by dividing by $(a+b)$

$60a=(a+b)t$ so $180a=3(a+b)t$

$90b=(a+b)t$ so $180b=2(a+b)t$

Add:

$180a+180b=3(a+b)t+2(a+b)t\Rightarrow180(a+b)=5(a+b)t$

Divide by $(a+b)$:

$180=5t\Rightarrow t=180\div5=36$