Two on five
Take 5 cubes of one colour and 2 of another colour. How many different ways can you join them if the 5 must touch the table and the 2 must not touch the table?
Problem
I've been playing around exploring what sort of shapes you can make with cubes. I particularly like those cubes that link together like Multilink ©. I'm sure that many of you have come across them or something similar.You can make all kinds of designs, perhaps pretending that you are making an animal or an alien or designing a house or some futuristic building or in fact, you can just imagine that you are creating rather interesting shapes and are happy with that.It is quite a good idea to set some sort of rule or rules that you have to follow and see how many models/designs you can make if you follow those rules.
I think a good challenge to start with is;
Use 7 of these cubes - 5 of them of one colour and 2 of another colour. These 7 have all to be joined together.
Now let's say that the cubes have to be joined "properly", that is with no twists, so a that a square face is flat against the next square face.So the two main rules that will control how we will build are as follows:-
The five that are of one colour must all touch the table that you are working on.
The two that are of a different colour must NOT touch the table.
Well, I wonder how many different designs you can discover or forecast?

Unless you have lots and lots, I really mean lots, of these cubes to use you will have to make a record of what you have done each time. This can be useful so that you can check that you have not done the same ones twice.
When you've done a few it would be good to see if there is a "system", or "particular way of working" that you are using or could use to make things easier.
Student Solutions
We see here some examples of Hayley's work. She recorded them in different ways but there is evidence of systems for generating new ones. She did very well to get 100, but there are more to do:

Here are all the 100 images:



Teachers' Resources
Why do this problem?
This investigation is one that uses the very popular multilink cubes. It gives a wonderful opportunity for pupils to explore ways of recording. This activity is also designed to nurture children's curiosity by introducing mathematics into a familiar non-mathematical context. Children might end up pursuing different ideas from each other and this freedom to explore may well encourage learners to persevere more than they might usually. In this way, they will immerse themselves in the particular number sequence they have chosen to use, which will help them gain a deep understanding of its structure. This activity lends itself to pupils posing their own questions in the form "I wonder what would happen if...?". (The further note at the foot of this page offers more support on curiosity in the classroom generally.)
Possible approach
You will need an awful lot of paper for the pupils' recording. I think, that as with many investigations, pupils should have the opportunities of recording in any way that they prefer. So, square dotted paper, triangular dotted paper, square paper both 2 cm and 1 cm, triangle marked paper as well as plain paper. It would be good if the children, as in most classes, have access to rulers, crayons, fibre tips, coloured sticky paper etc. etc.
I like to often introduce an investigation with a few words that might capture their imagination that sets the scene, so here goes:-
"Imagine that we are called on to design some modern buildings. The town in which they are to be built wants all of them to be different in the way that they look. There are to be seven rooms in these modern homes, all of them will be the same size, with five on the downstairs level and just two on the upstairs level. We have these cubes to use to help us make the designs. We really want to try to get as many different designs as possible." And, if that does not really appeal to you, then: "Let's imagine that we are here to create some models of interesting creatures from another planet that have to have five parts of their body touching the ground and the other two parts must not touch the ground." [Or anything else that you know as their teacher appeals to them in which the underlying rule is that five cubes must touch the ground and two cubes must not.]
I think it is good to carry on this introduction by getting five cubes of one colour and two of another colour, put five together in a "flat" shape resting on a surface that they can all see. Ask the pupils if that obeys the first rule about the five, then turn the shape around and ask if that obeys the rule. When you are satisfied that they have got that, you could ask some pupils to come and place the two "upstairs" cubes on it and check that everyone is quite happy with the two rules. This may seem to be rather unnecessary, but I do find that it avoids children being in the middle of an investigation and not being quite clear as to the rules.
So, with the rules in place and the pupils eager to get started the pupils are released from the group discussion and go off to have a go at the challenge.
Key questions
[Upon seeing a child who may be working some kind of system] "It looks as if you have some way of doing these, do have some ideas about what the next few are going to be like?"
[If they start to make them and are doing so confidently you can test going further] "If I ask you to simply describe to me in words what the next ones would be like, could you do that?"
Possible extension
Having done many solutions pupils could be asked to decide to make a change in the rules, i.e. try three on four or turning the two on five upside-down to have five on two.
For more extension work
Go to " 3 Sets of Cubes, 2 Surfaces" here.
Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:
The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.
Extras
I have used this activity with pupils aged from 6 to 12 years. There are a number of interesting approaches that I have witnessed [these are not in any particular order of sophistication or implication].
Some pupils:-
(a) start off with the five in a row and move all the twos around in a random manner and then go for other "base" shapes;
(b) make a shape and take it completely to pieces and then put them together in a new shape;
(c) take a base shape and keep the twos on top of each other and gradually move them along the shape and then move the twos around side by side, they then continue by separating the twos with one space between and try all the possibilities and then two spaces in between etc;
(d) make a base shape, place one of the twos at one end and then step by step move the second two from being on top to all the other four places that are available;
There are some variations that many children come across. Sometimes they ask "Are these allowed?". A good reply may be " Well, what are the rules that we are using? Do these keep the rules?".
Some pupils start in one way and then change the way that they are working. There is also quite often some good discussions on symmetry and whether it should be allowed or not. I usually allow each child to make up their own mind.
When deciding that they are making houses they point out sometimes that walking past the front of these two houses you see two different houses that are reflections (like a pair of semi-detached houses) but others who are working with the idea of just making shapes have some interesting ideas. I think that very often for the latter children there can be time given to reflect and the children may develop some of their spacial concepts much further than they were at the start of the challenge.
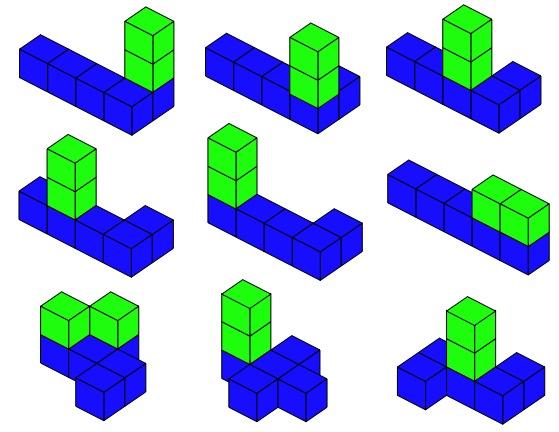
Some pupils :-
Make all the possibilities with a base shape, including the overhangs and then see whether there are the same number of arrangements for each different base, when exploring the small 'X' base they are surprised how few there are;
Have a really successful, confident time and then come across the '2' and the 'S' shape and cannot decide whether they are the same or not.
I have asked children who are working with a system and seem confident to imagine the models in their head and try to tell me how many of that style there are (perhaps on a particular base). When the time comes to an end I have always found they have thoroughly enjoyed themselves and are eager to talk about their thoughts and many of them can say a lot about their own ways of working. I sometimes talk about extensions when you might have three on top instead and ask what difference it would make.
If open, investigative challenges are something that you are a little wary of then this is certainly a good starter that should allow you to get the 'feel' of working investigatively.
