Triple Pythagoras
Can you work out the length of the diagonal of the cuboid?
Problem
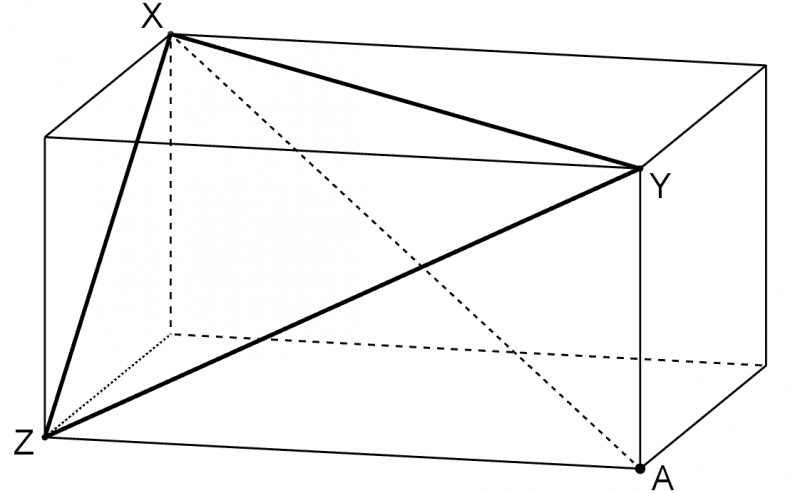
The diagram shows a cuboid.
In triangle XYZ, the lengths of XY, XZ and YZ are 9, 8 and $\sqrt{55}$ respectively.
What is the length of the diagonal XA?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
Let the lengths of the edges of the cuboid be $a$, $b$ and $c$, as shown in the diagram below.
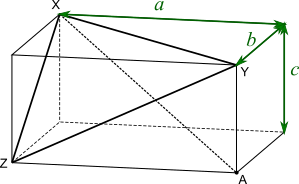
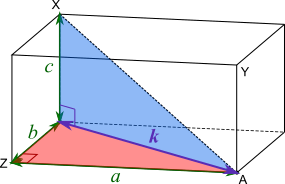
The required length $\text{XA}$ is the hypotenuse of the blue right-angled triangle in the diagram on the left, whose other sides are $c$ and $k$. So, by Pythagoras' theorem, $c^2+k^2=\text{XA}^2$.
The side labelled $k$ is also the hypotenuse of the red right-angled triangle, so $a^2+b^2=k^2$.
Substituting $a^2+b^2=k^2$ into $c^2+k^2=\text{XA}^2$ gives $c^2+a^2+b^2=\text{XA}^2$, so $\text{XA}^2=a^2+b^2+c^2$.
We can use Pythagoras' theorem on the other triangles to get more information about $a^2,$ $b^2$ and $c^2,$ and then use this to find $\text{XA}.$

$\text{XY}=9$, so, by applying Pythagoras' theorem to the yellow triangle in this diagram, $a^2+b^2=81$.

$\text{XZ}=8$, so, by applying Pythagoras' theorem to the yellow triangle in this diagram, $b^2+c^2=64$.
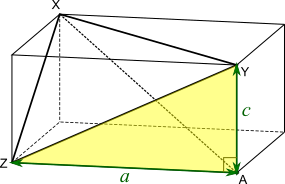
$\text{YZ}=\sqrt{55}$, so, by applying Pythagoras' theorem to the yellow triangle in this diagram, $a^2+c^2=55$.
Aiming for $\text{XA}^2=a^2+b^2+c^2$, we can get all three unknowns in the same equation by adding the equations $a^2+b^2=81$, $b^2+c^2=64$ and $a^2+c^2=55$: $$\begin{align}a^2+b^2+b^2+c^2+a^2+c^2&=81+64+55\\
\Rightarrow 2a^2+2b^2+2c^2&=200\\
\Rightarrow a^2+b^2+c^2&=100\\
\Rightarrow \text{XA}^2&=100\\
\Rightarrow \text{XA}&=10\end{align}$$
