Triangular teaser
Triangle T has sides of lengths 6, 5 and 5. Triangle U has sides of lengths 8, 5 and 5. What is the ratio of their areas?
Age
14 to 16
Challenge level
Problem
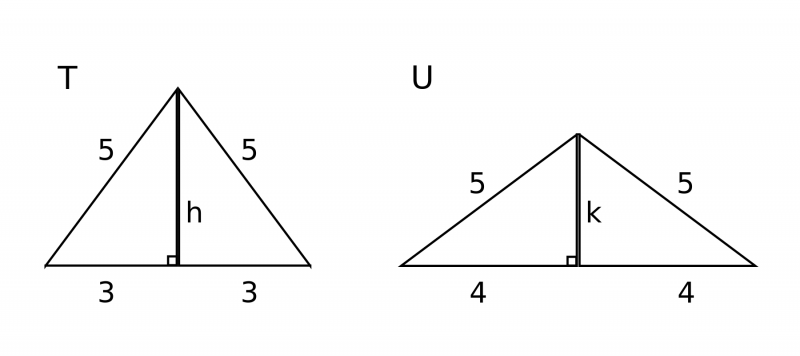
The triangle $T$ has sides of length $6$, $5$, $5$. The triangle $U$ has sides of length $8$, $5$, $5$.
What is the ratio area $T$ : area $U$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
The diagram below shows isosceles triangles $T$ and $U$. The perpendicular from the top vertex to the base divides an isosceles triangle into two congruent right-angled triangles as shown in both $T$ and $U$. Evidently, by Pythagoras' Theorem, $h = 4$ and $k = 3$. So both triangles $T$ and $U$ consist of two $3$, $4$, $5$ triangles and therefore have equal areas.
Image
