Triangle radius
Can you find the radii of the small circles?
Problem
The diagram below shows an equilateral triangle with side length 1.
The three circles inside the triangle are all tangent to each other and also to the triangle, and they all have the same radius.
What is the radius of the circles?
Leave your answer in surd form.
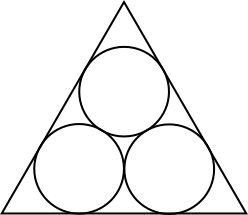
This problem is adapted from the World Mathematics Championships
Student Solutions
The circles are tangent to the triangle, so the radii shown below meet the triangle at right angles.
The circles are tangent to each other, so the line drawn connecting their centres is parallel to the base of the triangle.
The angle labelled is $30^\text{o}$ because, by the symmetry of the diagram, it is half of the $60^\text{o}$ angle in the equilateral triangle.
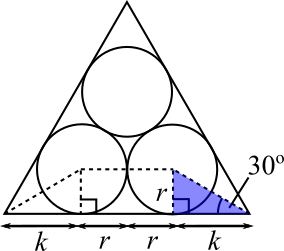
This means that in the diagram, there are two right-angled triangles and a rectangle enclosed by the dotted lines, and $2k+2r=1$.
From the blue triangle, $\tan{30}=\dfrac{r}{k}\Rightarrow k=\dfrac{r}{\tan{30}}=\sqrt{3}r$.
So $2k+2r=1\Rightarrow 2\sqrt{3}r+2r=1\Rightarrow r(2\sqrt{3}+2)=1 \Rightarrow r=\dfrac{1}{2+2\sqrt{3}}$
